Triângulos são polígonos que possuem três lados, três ângulos internos e três vértices. Eles estão presentes em diversos objetos do nosso dia a dia, fazendo com que seja muito importante o seu estudo.
A seguir, veja quais são as propriedades dos triângulos e entenda como utilizá-las em diferentes triângulos, só aqui no Gestão Educacional!
Propriedades dos triângulos com relação aos seus ângulos
Ângulo externo de um triângulo
Definimos ângulo externo como cada ângulo adjacentes e suplementar a um ângulo interno do triângulo.
Em um triângulo, existem três ângulos externos.
Observe a imagem abaixo. Os ângulos internos do triângulo estão representados em azul, enquanto os ângulos externos estão representados em amarelo.
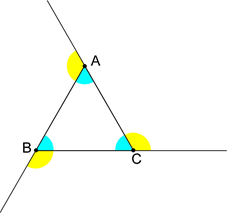
A seguir, veremos duas propriedades que usam os conceitos de ângulos internos e externos citados acima: a soma das medidas dos ângulos internos e externos.
Soma das medidas dos ângulos internos de um triângulo
A soma dos ângulos internos de um triângulo sempre será 180°.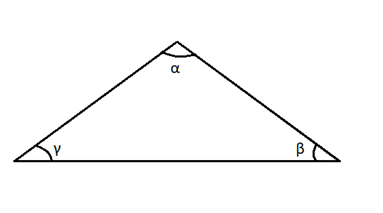
Observando o triângulo acima, podemos dizer que: α + β + γ = 180°.
Teorema do ângulo externo de um triângulo
Em todo triângulo, a medida de um ângulo externo é igual à soma das medidas dos ângulos internos e não adjacentes a ele.
Veja o esquema: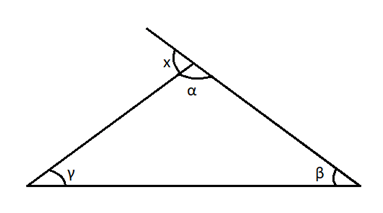
Os ângulos internos desse triângulo são α, β e γ, como mostra a figura.
Seja x um ângulo adjacente suplementar a α. Por definição, x é ângulo externo do triângulo, então: X + α = 180° (I).
Como sabemos que a soma dos ângulos internos de um triângulo será 180°, temos que: α + β + γ = 180° (II).
Observando (I) e (II), podemos concluir que: X = β + γ. Ou seja, a medida do ângulo externo x é igual à soma dos ângulos internos não adjacentes β e γ.
Outras importantes propriedades que podem ser aplicadas a todos os triângulos estão a seguir:
- A soma dos ângulos externos sempre será 360°;
- O lado que possui a menor medida será o lado oposto ao menor ângulo interno;
- O lado que possui a maior medida será o lado oposto ao maior ângulo interno.
Relações métricas em um triângulo qualquer
Existem duas relações métricas que se aplicam a qualquer triângulo: lei dos cossenos e lei dos senos. Veja, a seguir, as duas relações.
Lei dos cossenos
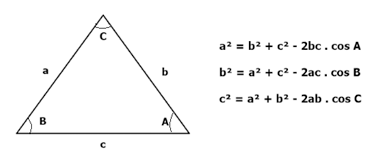
Em um triângulo, o quadrado da medida de um lado é igual à soma dos quadrados das medidas dos outros dois lados, menos duas vezes o produto das medidas desses lados pelo cosseno do ângulo que eles formam. Ou seja:
- a² = b² + c² – 2bc . cos A;
- b² = a² + c² – 2ac . cos B;
- c² = a² + b² – 2ab . cos C.
Lei dos senos
Em qualquer triângulo, as medidas dos lados são proporcionais aos senos dos ângulos opostos, ou seja: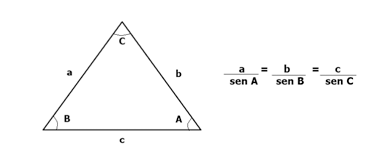
Classificação de um triângulo pela medida de seus ângulos
O triângulo abaixo possui seus lados com medidas a, b e c e ângulos internos de valores iguais a A, B e C.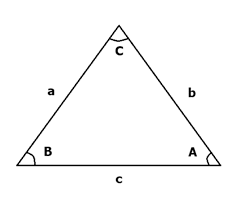
Um triângulo pode ser:
- Acutângulo: quando os ângulos A, B e C são agudos;
- Retângulo: quando apenas um dos ângulos A, B ou C é reto;
- Obtusângulo: quando apenas um dos ângulos A, B ou C é obtuso.
Porém, como podemos classificar um triângulo quando conhecemos apenas as medidas dos seus lados?
Vamos admitir que a seja a medida do maior lado do triângulo. Então: a ≥ b e a ≥ c.
Sabendo que o maior lado se opõe ao maior ângulo, então: A ≥ B e A ≥ C.
Concluímos, portanto, que, se a é o maior lado do triângulo ABC e o ângulo A é o maior ângulo.
Nessa situação, pensando na medida do ângulo A, temos que:
- ΔABC é retângulo somente se A = 90°;
- ΔABC é acutângulo somente se A < 90°;
- ΔABC é obtusângulo somente se A > 90°.
Quanto à medida dos lados, podemos concluir que:
- ΔABC é retângulo somente se a² = b² + c² ;
- ΔABC é acutângulo somente se a² < b² + c²;
- ΔABC é obtusângulo somente se a² < b² + c².
Resumindo, podemos formar a seguinte tabela sobre classificação dos triângulos quanto aos seus ângulos e aos seus lados: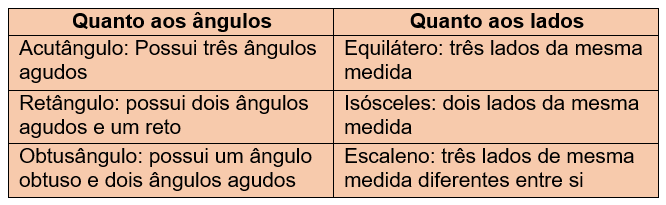
Propriedades específicas de cada triângulo
A seguir, veja as propriedades de cada triângulo:
- Isósceles: os ângulos da base possuem a mesma medida;
- Equilátero: os três ângulos internos têm a mesma medida, que no caso é 60°;
- Retângulo: a medida dos seus lados pode ser relacionada pelo Teorema de Pitágoras;
- Escaleno: a soma dos seus ângulos internos é igual a 180º.
Pontos notáveis de um triângulo
- Baricentro: as três medianas de um triângulo se interceptam num mesmo ponto, chamado de baricentro;
- Incentro: as três bissetrizes internas de um triângulo se interceptam num mesmo ponto, chamado de incentro;
- Circuncentro: ponto de intersecção das mediatrizes dos lados de um triângulo;
- Ortocentro: ponto de encontro das três alturas do triângulo.
