Registros em antigos papiros já apresentavam problemas com quantidades desconhecidas e alguns métodos de resolução. Por volta de 825, o matemático árabe al-Khowarizmi propôs uma organização de termos para chegar à solução de uma equação, inaugurando a “ciência das equações”.
Ao longo de 3 mil anos, diversos estudiosos desenvolveram gradualmente símbolos para representar as equações algébricas, e até hoje gostamos de utilizar o x.
O matemático italiano Paolo Ruffini confirmou que não existia fórmula para a resolução de equações de grau superior a 4. E o que veremos a seguir são polinômios e como encontrar as suas raízes.
Definição de polinômio
Chamamos expressão polinomial ou polinômio na variável complexa x toda expressão da forma: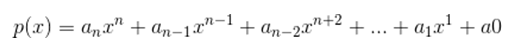
Exemplos:
- a) p(x) = 5 é um polinômio de grau 0 ou polinômio constante;
- b) p(x) = 2x – 1 é um polinômio do 1º grau;
- c) p(x) = x² + 5x + 6 é um polinômio do 2º grau.
Para não ser expressão polinomial, o expoente da variável x não pode ser negativo ou fracionário e a variável x não pode estar no denominador ou aparecer sob radical.
Valor numérico, igualdade e raízes de polinômios
Considere o polinômio p(x) e o número real α. O valor numérico do polinômio p(x) para x = α é o número que se obtém substituindo x por α e efetuando os cálculos necessários. Então, p(α) é o valor numérico para p(x) para x = α.
Exemplo: O valor numérico de p(x) = -2x² – 3x + 5 para x = 4 é:
p(4) = 2(4)² – 3(4) + 5 = 25.
Logo, p(4) = 25.
- Dois polinômios p(x) e q(x) são iguais se, e somente se, possuem coeficientes dos termos de mesmo grau iguais.
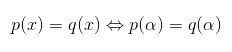Para qualquer α pertencente aos complexos.
- Se um número complexo α é tal que p(α) = 0, então esse número α é chamado de raiz do polinômio.
Exemplo: Dado o polinômio p(x) = -x² – 7x + 10, temos:
p(5) = 0 ⇒ 5 é raiz de p(x)
p(3) = 22 ⇒ 3 não é raiz de p(x).
Divisão de polinômios
Dados dois polinômios p(x) e h(x) não nulo, dividir p(x) por h(x) significa encontrar polinômios q(x) e r(x) que satisfaçam as duas condições: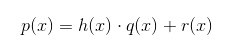
Sendo:
- p(x) é o dividendo;
- h(x) é o divisor;
- q(x) é o quociente;
- r(x) é o resto.
Segundo, o grau de r(x) não pode ser igual nem maior do que o grau de h(x) ou então r(x)=0.
Para efetuar a divisão de polinômios, usaremos o método da chave, semelhante ao empregado para números inteiros.
Para entender o método da chave, veja o seguinte vídeo e observe os exemplos:
Quando r(x) = 0 (o resto da divisão é igual a zero), dizemos que a divisão é exata e o polinômio p(x) é divisível pelos polinômios h(x) e q(x).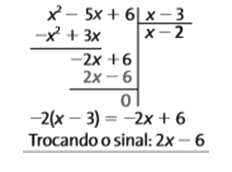
Veja, a seguir, outro exemplo: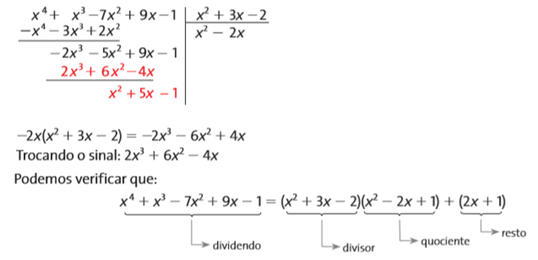
Dispositivo prático: Briot-Ruffini
Usando o método da chave, podemos efetuar a divisão entre dois polinômios. Porém, há um dispositivo que permite efetuar as divisões dos polinômios do tipo (x – a) de uma maneira mais simples e rápida: o algoritmo de Briot-Ruffini. Esse método faz com que o resto seja sempre uma constante.
Vamos ver como funciona esse dispositivo efetuando a divisão de p(x) = 3x³ – 5x² + x – 2 por h(x) = x – 2.
Primeiramente, iremos montar o dispositivo:
Sendo:
- O termo constante do divisor h(x) igual a –2, ele com sinal trocado será 2;
- Os coeficientes de x do dividendo p(x) são 3, -5 e 1;
- O termo constante do dividendo p(x) = -2.
Montaremos o dispositivo da seguinte maneira: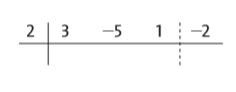
Agora, repetimos ou “abaixamos” o primeiro coeficiente do dividendo:
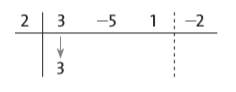Multiplicamos o termo repetido pelo divisor e somamos o produto com o próximo termo do dividendo:
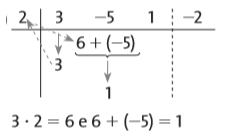Repetimos o processo para obter o novo termo do quociente:
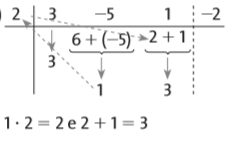No final, teremos:
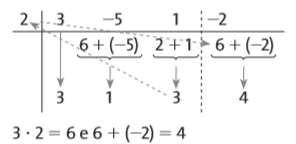Pelo resultado acima, temos:
- q(x) = 3x² + 1x + 3;
- r(x) = 4;
- h(x) = x – 2.
Logo, temos que: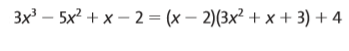
Para entender melhor, você pode assistir o seguinte vídeo:
Raízes de uma equação polinomial
Pelo Teorema do Fator, sabemos que se c é uma das raízes do polinômio p(x), consequentemente p(c) = 0. Além disso, temos: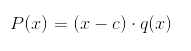
Portanto, (x – c) é um fator de p(x).
Ou seja: se (x-c) é fator de p(x), então c é raiz do polinômio p(x).
Sabemos encontrar facilmente raízes de equações do primeiro e segundo grau. Porém, verificou-se que o melhor jeito de encontrar essas raízes em equações de grau 3 ou 4 é fazendo estimativas. Existem, então, alguns métodos que ajudam nisso.
Podemos fazer a decomposição em fatores de primeiro grau. Ou seja: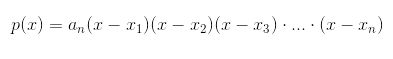
Portanto, se p(x) = 0, concluímos que:
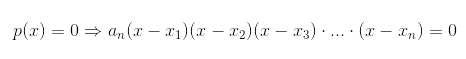Veja, a seguir, os métodos que utilizamos para encontrar raízes nas equações até o quarto grau.
Raízes nas equações
- Segundo grau
Dada a equação algébrica ax² + bx + c = 0, suas raízes x1 e x2 podem ser encontradas quando é satisfeito: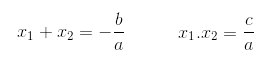
- Terceiro Grau
Dada a equação ax³ + bx² + cx + d = 0, suas raízes x1, x2 e x3 são encontradas quando é satisfeito: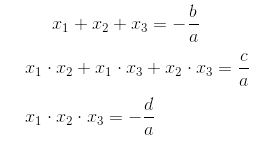
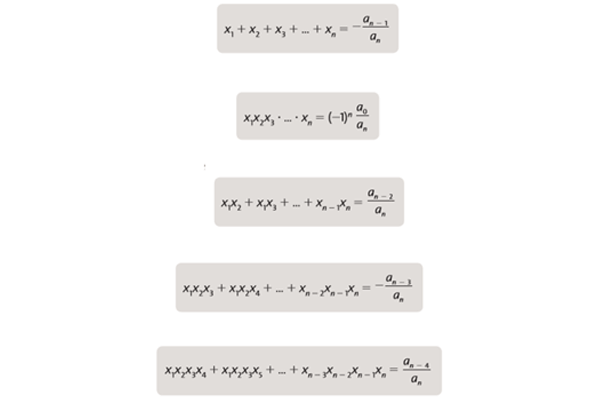
- Equação de grau n
Dada a equação algébrica 
de raízes x1, x2, … , xn, são validas as seguintes relações, conhecidas como Relações de Girard:
