O movimento retilíneo uniformemente variado é um tipo de movimento no qual temos uma variação da velocidade de acordo com o passar do tempo, devido a uma aceleração constante. Ou seja, existem duas grandezas que variam com o tempo: velocidade e posição.
Nesse tipo de movimento conseguimos estudar as quatro grandezas da física que são mais relevantes: aceleração, velocidade, espaço e tempo.
Quando temos uma variação de velocidade igual em intervalos de tempo iguais, podemos dizer que o movimento estudado é uniformemente variado. Veja, a seguir, como funciona esse movimento, quais são as fórmulas utilizadas e como resolver exercícios sobre ele. Só aqui no Gestão Educacional!
Aceleração média e instantânea
A aceleração está diretamente ligada à variação da velocidade. Portanto, definimos variação na física como a razão entre a variação da velocidade e a variação do tempo em uma trajetória.
A fórmula usada para calcular é: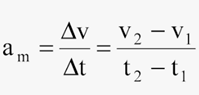 Nessa fórmula, temos:
Nessa fórmula, temos:
- Δv = variação de velocidade = velocidade final – velocidade inicial;
- Δt = variação do tempo = instante final – instante inicial.
A unidade de medida da aceleração no SI é m/s². Por exemplo, se um móvel tem uma aceleração de 5 m/s², podemos dizer que a cada segundo sua velocidade varia 5 m/s.
Porém, além disso, precisamos diferenciar dois importantes conceitos:
- Diferença entre aceleração média e aceleração constante: a aceleração média é a aceleração do móvel calculada em um intervalo de tempo. Enquanto isso, a aceleração instantânea é calculada em um intervalo de tempo muito pequeno, praticamente um instante. Isso ocorre quando Δt tende a zero, ou seja, a um instante bem pequeno.
Exercícios resolvidos
1) Um automóvel está com velocidade de 90 km/h quando é freado em linha reta, parando em 5,0s. Determine a aceleração média ocorrida durante a frenagem em m/s².
RESPOSTA:
Considerando que a velocidade final é v = 0 porque o carro freou e o instante inicial é t0 = 0s, usaremos a fórmula da aceleração média.
Primeiramente, vamos converter a velocidade que está em km/h para m/s.
Vo = 90/3,6 = 25 m/s.
Aplicando essas informações na fórmula: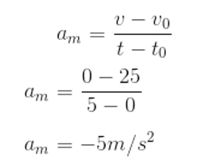
Função da velocidade em relação ao tempo
Podemos escrever a função da velocidade em relação ao tempo t de um ponto material em MRUV a partir da expressão que vimos sobre a aceleração.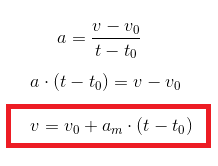 Essa função também pode ser escrita da seguinte maneira:
Essa função também pode ser escrita da seguinte maneira: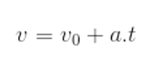
Função da posição em relação ao tempo
A função da posição x de um ponto material em relação ao tempo t em MRUV é dada pela expressão: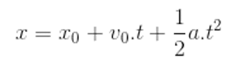
Equação de Torricelli
Em problemas que relacionam a distância percorrida com a velocidade do veículo, costumamos utilizar outra equação. Nesse caso, não é necessário conhecer o tempo em que o percurso foi feito.
A função que relaciona a velocidade de um ponto material e sua posição é dada por: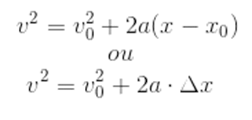 Sendo:
Sendo:
- V = velocidade final;
- V0 = velocidade inicial;
- a = aceleração;
- Δx = x – x0 = espaço percorrido.
Exercício resolvido
2) Um automóvel parte do repouso em movimento retilíneo com aceleração constante de 2,0 m/s². Qual a velocidade desse automóvel, em km/h, após um percurso de 100m?
RESPOSTA:
Sendo v0 = 0, a = 2m/s² e Δx = 10 m, vamos utilizar a função da velocidade em relação ao deslocamento: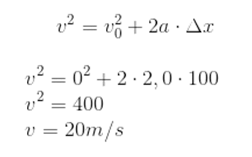 Convertendo a velocidade de m/s para km/h, temos: V = 20 . 3,6 = 72 km/h.
Convertendo a velocidade de m/s para km/h, temos: V = 20 . 3,6 = 72 km/h.
Gráfico do MRUV
Os gráficos são uma ótima alternativa para o estudo desse movimento, pois permitem uma melhor visualização da forma como variam as grandezas do movimento. Conheça os dois tipos de gráfico mais utilizados no MRUV:
Gráfico velocidade x tempo
Esse gráfico possui, no eixo das abscissas, a variação de tempo e, no eixo das ordenadas, a variação da velocidade. São grandezas que se relacionam linearmente, portanto, esse gráfico será uma reta, na qual iremos calcular o coeficiente linear (m) da seguinte maneira: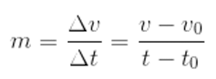 Já vimos algo parecido acima. Portanto, o coeficiente angular desse gráfico é a aceleração.
Já vimos algo parecido acima. Portanto, o coeficiente angular desse gráfico é a aceleração.
Quando a aceleração é positiva, ou seja, o sentido da aceleração coincide com o eixo, o coeficiente angular é positivo e o gráfico é de uma função crescente. Porém, quando a aceleração é negativa, ela tem sentido oposto ao do eixo e o gráfico é de uma função decrescente.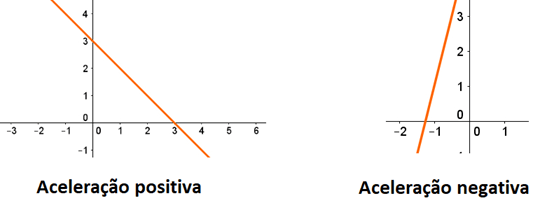 No MRUV, a área abaixo da curva do gráfico velocidade x tempo no intervalo de tempo Δt é igual ao deslocamento Δx.
No MRUV, a área abaixo da curva do gráfico velocidade x tempo no intervalo de tempo Δt é igual ao deslocamento Δx.
Portanto, podemos escrever que: A = Δx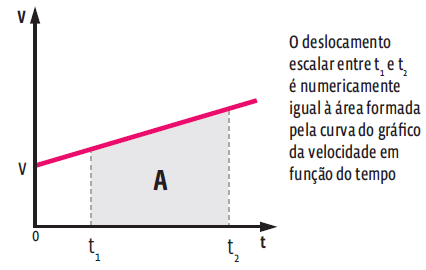
Gráfico da posição x tempo
A função da posição em relação ao tempo é uma função do segundo grau.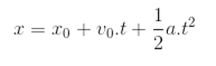 Como a concavidade da parábola depende do sinal de t² e esse sinal depende do sinal da aceleração, podemos concluir que a concavidade da parábola depende do sinal da aceleração.
Como a concavidade da parábola depende do sinal de t² e esse sinal depende do sinal da aceleração, podemos concluir que a concavidade da parábola depende do sinal da aceleração.
Quando a aceleração é positiva, a concavidade é voltada para cima; quando é negativa, a concavidade é voltada para baixo. Para visualizarmos melhor isso, observe a imagem abaixo.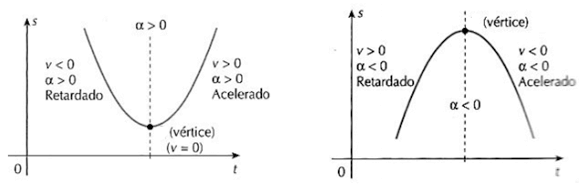 Do lado esquerdo, temos um exemplo no qual a aceleração é positiva, formando uma parábola com concavidade para cima. Do lado direito, temos uma parábola que mostra um movimento de aceleração negativa, portanto, sua concavidade é voltada para baixo.
Do lado esquerdo, temos um exemplo no qual a aceleração é positiva, formando uma parábola com concavidade para cima. Do lado direito, temos uma parábola que mostra um movimento de aceleração negativa, portanto, sua concavidade é voltada para baixo.

