Chamamos de função quadrática a função polinomial de segundo grau, dada pela seguinte lei de formação: f(x) = ax² + bx +c, sendo a, b e c números reais e a ≠ 0. O gráfico dessa função é uma parábola, que pode interceptar o eixo x em nenhum, um ou até dois pontos. Esses pontos são o que chamamos de raízes ou zeros da equação.
O cientista italiano Galileu Galilei analisou o movimento de objetos em queda no campo gravitacional da Terra e concluiu que, se não fosse a resistência do ar, o espaço percorrido por esses corpos seria proporcional ao quadrado do tempo de percurso. Dessa maneira, Galileu criou o conceito que hoje chamamos de função quadrática.
Raízes da função – Zeros da função
Para encontrarmos as raízes da função quadrática, devemos determinar os valores de x para os quais a função se anula, ou seja, f(x) = 0: ax² + bx + c = 0.
Existem alguns métodos para fazermos isso. Veremos dois, a seguir: a Bhaskara e a soma e produto.
Fórmula de Bhaskara
Para calcular os zeros de uma função quadrática, podemos utilizar esse método, desde que sejam conhecidos os coeficientes dessa equação.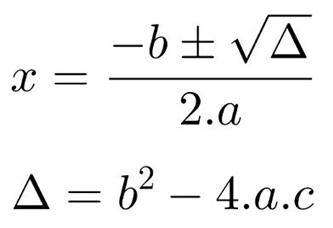
O número Δ = b² – 4.a.c é chamado de discriminante da função quadrática f(x) = ax² + bx +c.
Quando:
- Δ > 0, a função f(x) = ax² + bx + c tem dois zeros reais diferentes;
- Δ = 0, a função f(x) = ax² + bx + c tem um zero real duplo;
- Δ < 0, a função f(x) = ax² + bx + c não tem zeros reais.
Soma e produto
Existindo raízes reais (quando Δ ≥ 0), podemos encontrá-las utilizando o método de soma e produto.
Sendo x1 e x2 as raízes da função f(x) = ax² + bx + c, faremos:
Ou seja, precisamos encontrar dois números que somados resultem em -b/a e o produto deles resulte em c/a.
Por exemplo, dada a função f(x) = x² -5x + 6, vamos encontrar os zeros dessa função pelo método da soma e do produto.
Sendo a = 1, b = -5 e c = 6, faremos:
x1 + x2 = – (-5)/1
x1 + x2 = 5
X1 . X2 = 6/1
x1 . x2 = 6
Ou seja, estamos tentando encontrar dois números que, quando somados, resultam em 5 e, quando multiplicados, resultam em 6. Sabemos que 2.3 = 6 e também que 2 + 3 = 5. Portanto, as duas raízes dessa equação são x1 = 2 e x2 = 3.
Forma fatorada da função quadrática
Quando Δ ≥ 0, ou seja, quando a equação ax² + bx c = 0 possui raízes reais x1 e x2, podemos escrever essa equação em sua forma fatorada, dada por: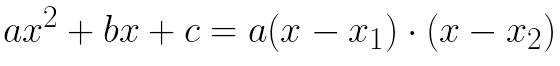
Gráfico da função quadrática
O gráfico de uma função quadrática será sempre uma parábola. Caso a função seja definida por f(x) = ax² + bx + c, cada um dos parâmetros a, b e c irão exercer certo efeito na aparência dessa parábola.
- Parâmetro a
Esse parâmetro é responsável pela concavidade e pela abertura da parábola.
Além disso, quanto maior é o valor absoluto do parâmetro a, maior será a abertura da parábola.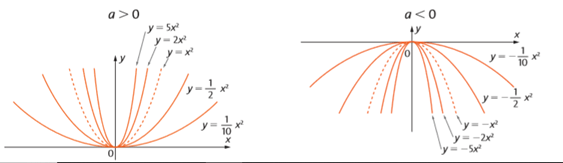 
- Parâmetro b
Esse parâmetro indica se a parábola intersecta o eixo y no ramo crescente ou decrescente da parábola.
Nesse caso, temos três efeitos: quando b < 0, quando b > 0 e quando b = 0.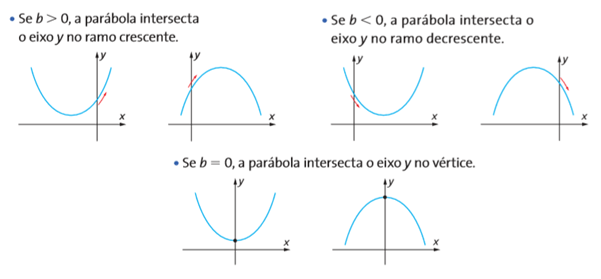
- Parâmetro c
O valor de c indica o ponto onde a parábola intersecta o eixo y. Ou seja, ela intersecta o eixo y no ponto (0,c). Portanto: f(0) = c.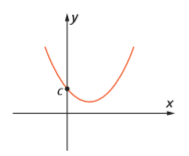
Pontos de intersecção com os eixos
A parábola da função quadrática f(x) = ax² + bx + c intercepta o eixo y sempre no ponto (0,c).
Porém, essa parábola pode interceptar o eixo x em apenas um ponto, em dois pontos e até mesmo em nenhum ponto. Para descobrir isso, basta conferir o valor de Δ:
- Δ = 0: a parábola intercepta o eixo x em um só ponto, pois tem uma raiz real dupla;
- Δ > 0: a parábola intercepta o eixo x em dois pontos, pois possui duas raízes distintas;
- Δ < 0: a parábola não intercepta o eixo x, pois não tem raiz real.
Máximo, mínimo e vértice da parábola
Podemos calcular as coordenadas do vértice da parábola f(x) = ax² + bx + c da seguinte maneira: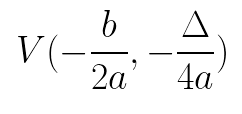
Quando a parábola possui sua concavidade voltada para cima, o valor de y do vértice é um ponto de mínimo dessa função.
Porém, quando a concavidade é voltada para baixo, o valor de y do vértice é o ponto de máximo dessa função.
Portanto:
- a > 0: yv é valor de mínimo;
- a < 0: yv é valor de máximo.
