Utilizamos o arranjo simples quando queremos saber quantos agrupamentos ordenados diferentes podemos formar com p dos n elementos dados, sendo sempre p ≤ n. Ou seja, nesse caso, a ordem em que os elementos se encontram no agrupamento é importante.
Um dos métodos mais antigos de criptografia, utilizado desde a antiguidade, é alterar a posição dos elementos, tornando a mensagem ilegível. Atualmente, com a tecnologia da análise combinatória, o uso da criptografia ficou mais sofisticado. Hoje, informações codificadas expandiram-se: estão presentes em cartões de crédito, na internet e até mesmo em ligações telefônicas.
O que é um arranjo simples?
Por exemplo: usando os algarismos 2, 3, 5, 7 e 9, quantos números naturais de 3 algarismos distintos podemos formar? Para isso, podemos utilizar o seguinte raciocínio:
A primeira posição será utilizada para os números da centena; a segunda para os números da dezena; e, por último, para os números das unidades. Ao todo, temos 5 números que podem ser usados para preencher as posições.
Como não podemos repetir, há 5 possibilidades para o 1º algarismo, 4 para o 2º e 3 para o 1º. No total, podemos formar 5 . 4 . 3 = 60 números.
Podemos também obter esse mesmo resultado utilizando a fórmula do arranjo: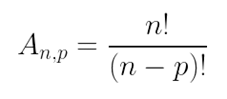
Sendo:
- n = número total de elementos;
- p = números de elementos que queremos que estejam no agrupamento ordenado.
Resolvendo o exemplo acima, utilizando a fórmula, teremos n = 5 e p = 3: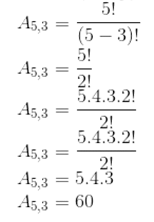
Veja: sempre teremos n ≥ p. Ou seja, o número de elementos ao todo deve ser maior ou igual ao número de elementos dos agrupamentos que queremos fazer.
Diferença entre arranjo e combinação
Quando realizamos a combinação de n elementos em grupos de p elementos, sem se importar com a ordem dos elementos nesse grupo, estamos fazendo a combinação desses elementos. Porém, quando a ordem é importante, precisamos utilizar o arranjo.
Podemos visualizar isso melhor imaginando a seguinte situação:
(1) Anna, Elisa, Rosana, Diego, Fabrício e João estão disputando uma corrida. Quais são as possibilidades de formação do pódio de primeiro, segundo e terceiro lugar?
Nesse caso, a posição em que cada pessoa fica faz diferença: se eles ficam em primeiro, segundo ou terceiro é diferente.
Porém, se essas mesmas pessoas estiverem se organizando em duplas para treinar para esse campeonato, tanto faz se a dupla for (Anna, Elisa) ou (Elisa, Anna). Portanto, a ordem não importa. Nesse caso, usaremos, então, a combinação.
Como resolver exercícios de arranjo?
Todos os exercícios que envolvem arranjo simples podem ser resolvidos de duas formas: utilizando a fórmula e usando um raciocínio de multiplicar os números usados em cada posição. Essas duas maneiras foram empregadas na resolução do primeiro exemplo. Veja outros exemplos, a seguir, nos exercícios resolvidos.
Exercícios resolvidos
1) Quantos números de dois algarismos diferentes podemos escrever com algarismos 1, 2, 3, 4, 5, 6, 7, 8 e 9?
RESPOSTA:
1ª maneira: utilizando a fórmula.
Procuramos agrupamentos de 2 elementos em que a ordem é importante, pois, por exemplo, 12 ≠ 21. Temos 9 elementos para serem arranjados 2 a 2. Assim, temos que calcular: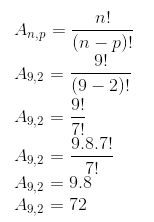
Portanto, existem 72 números de dois algarismos diferentes que podem ser escritos com os algarismos de 1 a 9.
2ª maneira: sem usar a fórmula.
Para o algarismo das dezenas, temos 9 opções e, para algarismo das unidades, apenas 8 opções, pois não podemos repetir algarismos.
Assim, temos 9 . 8 = 72 possibilidades.
Portanto, são 72 números.
2) Quantos números de 2 algarismos diferentes podemos escrever com os algarismos 1, 2, 3 e 4?
RESPOSTA:
1ª maneira: sem usar a fórmula.
Para o algarismo das dezenas, temos 4 opções e, para o algarismo das unidades, apenas 3, pois não podemos repetir algarismos. Assim, temos 4 . 3 = 12 possibilidades, portanto, 12 números.
2ª maneira: utilizando a fórmula.
Nesse caso, temos quatro dígitos, 1, 2, 3 e 4, e queremos saber quantos números de 2 algarismos diferentes podemos escrever com eles. Precisamos calcular A4,2.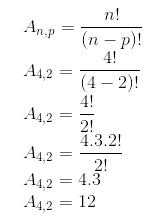
Portanto, podemos escrever 12 números com 2 algarismos diferentes com os dígitos 1, 2, 3 e 4.
3) Um estudante tem 5 lápis de cores diferentes. Quantas maneiras diferentes ele poderá pintar os estados da região Sul do Brasil, cada um de uma cor?
RESPOSTA:
1ª maneira: sem usar a fórmula.
São 3 estados: Rio Grande do Sul, Paraná e Santa Catarina. Para pintar o Rio Grande do Sul, há 5 possibilidades, para o Paraná, 4 possibilidades, e, para Santa Catarina, 3 possibilidades.
Logo, 5 . 4 . 3 = 60 possibilidades.
2ª maneira: usando a fórmula.
Os estados do sul do Brasil são 3: Paraná, Santa Catarina e Rio Grande do Sul. Logo, devemos calcular A5,3.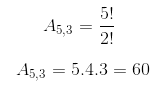
Portanto, há 60 maneiras diferentes de pintar os estados do Sul usando 5 cores.
