Permutação simples – O que é? Exemplos e Exercícios resolvidos!

Por

Permutar é sinônimo de trocar a ordem, embaralhar, trocar objetos de posição. Quando calculamos a permutação de um número de objetos, estamos calculando quantos agrupamentos são possíveis de formar com esses elementos, usando todos em cada agrupamento.

A permutação simples é igual à fatorial de um número. Dado um número inteiro, a permutação simples desse número será a multiplicação dele mesmo e de seus antecessores inteiros até o número 1.

Princípio fundamental da contagem

A partir do que chamamos de árvore de possibilidades, podemos, por exemplo, saber quantos números de 3 algarismos podemos formar com os algarismos 1, 2 e 3, sem repeti-los num mesmo número.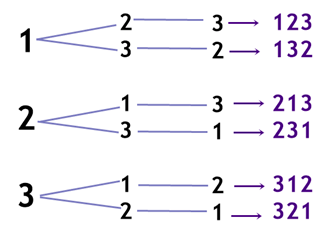Permutação simplesAssim, temos: 123, 132, 213, 231, 312 e 321. Pelo princípio fundamental da contagem, são 3 . 2 . 1 = 6 possibilidades.

Observe que a ordem dos algarismos é algo importante, ou seja, todos os números diferem entre si pela ordem de seus algarismos.

Usamos a permutação simples para: resolver exercícios que pedem anagramas; organizar objetos em diferentes lugares; formar números naturais de algarismos distintos, entre outros problemas que troquem a ordem de todos os objetos do conjunto.

O que é permutação simples?

Se temos n elementos distintos, então o número de agrupamentos ordenados (diferentes pela ordem) que podemos obter com todos esses n elementos é dado por: Pn = n . (n – 1) . (n – 2) . … . 3 . 2 . 1 = n!

Exemplos

  • P5 = 5 . 4 . 3 . 2 . 1 = 120;
  • P2 = 2 . 1 = 2;
  • P8 = 8 . 7 . 6 . 5 . 4 . 3 . 2 . 1 = 40.320.

Exercícios resolvidos

1) De quantas maneiras podem ser arrumados de forma horizontal três selos: 1 da Argentina, 1 do Brasil e 1 do Chile? Quais são essas maneiras?

RESOLUÇÃO:

Vamos indicar o selo da Argentina por A, do Brasil por B e do Chile por C. Podemos assim construir a árvore de possibilidades: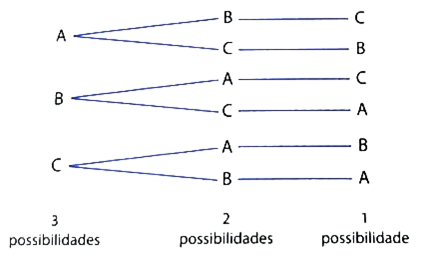Permutação simplesUsando o princípio fundamental da contagem, temos: 3! = 3 . 2 . 1 = 6 possibilidades.

Logo, é possível arrumar os três selos de 6 maneiras diferentes.

Os agrupamentos ordenados são: ABC, ACB, BAC, BCA, CAB, CBA.

2) De quantas maneiras uma família de 5 pessoas pode se sentar num banco de 5 lugares para tirar uma foto?

Resolução:

Nesse exercício, vamos utilizar a permutação simples P5 para descobrir:

P5 = 5 . 4 . 3 . 2 . 1 = 120 maneiras.

3) Responda:

  1. a) Quantos são os anagramas da palavra PERDÃO?
  2. b) Quantos são os anagramas da palavra perdão que começam com P e terminam com O?

c)Quantos são os anagramas da palavra perdão em que as letras PER aparecem juntas, em qualquer ordem?

  1. d) Quantos são os anagramas da palavra PERDÃO em que A e O aparecem juntas nessa ordem?
  2. e) Quais são os anagramas em que P e O aparecem nos extremos?

Resolução:

  1. a) Basta calcular 6! = 6 . 5 . 4 . 3 . 2 . 1 = 720.
  2. b) Anagramas iniciados com P e terminados com O:

P _ _ _ _ O

Devemos permutar quatro letras que não são fixas, sendo elas E, R, D e Ã.

4!  = 4 . 3 . 2 . 1 = 24 anagramas.

  1. c) Considerando PER como uma só letra, temos outras três letras restantes para permutar além dessa consideração.

Faremos:

P4 = 4! = 4 . 3 . 2 . 1 = 24 possibilidades.

Como as três letras de PER podem aparecer em qualquer ordem, temos P3 = 3! = 3 . 2 . 1 = 6 possibilidades de escreve-las juntas.

Assim, o número total de anagramas pedido é:

4! . 3! = 24 . 6 = 144 anagramas.

  1. d) Vamos considerar que a expressão ÃO é uma só letra. Restam ainda quatro letras para serem permutadas além dessa. Vamos, portanto, fazer uma permutação de 5 letras:

P5 = 5 . 4 . 3 . 2 . 1 = 120 anagramas.

  1. e) Quando P e O aparecem nos extremos, dois casos podem acontecer:

P _ _ _ _ O

Ou

O _ _ _ _ P

Temos o primeiro caso no qual vamos permutar quatro letras. Em seguida, somamos com a permutação de quatro letras no segundo caso:

P4 + P4 = 2.P4 = 2 . 4! = 2 . 4 . 3 . 2 . 1 = 2 . 24 = 48 anagramas.

Deixe um comentário