Vetores são uma classe de equipolência de seguimentos orientados. São usados para representar grandezas vetoriais. Para indicarmos um vetor, usamos letras com uma seta acima delas.
Existem grandezas chamadas escalares, que são caracterizadas por um número e a unidade correspondente, como 50 dm² de área, 4 m de comprimento, 7 kg de massa. No entanto, há outras grandezas que precisam mais do que isso, por exemplo, uma força ou velocidade. Essas são grandezas chamadas vetoriais.
Representação de grandezas vetoriais: o vetor
Para representar grandezas vetoriais, utilizamos o vetor. O vetor possui:
- Intensidade ou módulo;
- Direção;
- Sentido.
Ele pode ser representado por um seguimento de reta orientado, cujo comprimento indica o módulo. A reta s suporte indica a direção e a seta indica o sentido.
Para entender melhor, os vetores abaixo possuem a mesma direção e o mesmo sentido: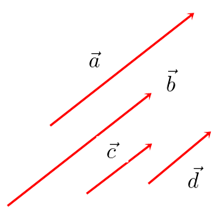
Porém, os vetores a seguir possuem a mesma direção, mas sentidos opostos.
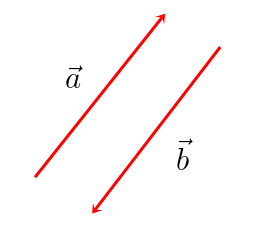Com isso, percebemos que dois vetores que possuem a mesma direção são representados por setas paralelas.
A representação de uma grandeza vetorial é dada pelo acréscimo de uma seta sobre o símbolo que a representa. Por exemplo, representamos uma força de 20N que é aplicada em um bloco por: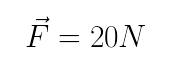
Veja como um vetor pode ser representado: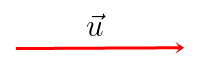
- Chamamos de nulo um vetor cuja origem e extremidade são as mesmas. Ele pode ser representado por 0 com seta em cima;
- Indicamos que dois vetores x e y são paralelos, usando a seguinte notação: x \\ y;
- O vetor nulo é paralelo a qualquer outro veto;
- Chamamos de norma o módulo ou comprimento de um vetor. Ela é indicada por: se a norma for 1, dizemos que esse vetor é unitário.
Adição de vetores
Vetores com a mesma direção
Se dois vetores possuem a mesma direção, estabelecemos um sentido como positivo e outro como negativo. Somamos algebricamente os seus módulos.
Por exemplo, vamos somar os vetores da figura abaixo. Convencionando como o sentido positivo o horizontal para a direita, vamos atribuir o sinal positivo para os vetores a e b e o módulo de c com sinal negativo. A soma será um vetor d, cujo módulo é: d = a + b – c.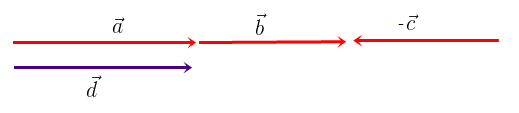
Se o módulo do vetor resultante d for positivo, ele é horizontal para a direita. Caso negativo, ele é horizontal para a esquerda.
Soma de vetores em direções quaisquer
Para isso, podemos utilizar duas regras: fechar o triângulo ou a regra do paralelogramo.
Para somar os vetores abaixo, basta colocar a extremidade final de um ligada à extremidade inicial de outro. O vetor resultante será o vetor que “fecha” esse triângulo, como mostra a figura: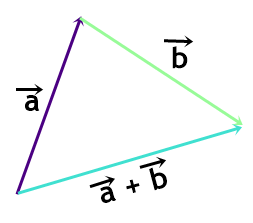
Além disso, podemos usar a regra do paralelogramo. A diagonal do paralelogramo, cujos lados são os vetores a e b, é o vetor resultante c. Observe a figura:
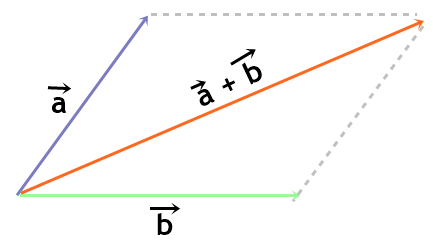Se a e b formam entre si um ângulo α, o módulo do vetor resultante a + b é dado pela expressão: c² = a² + b² + 2ab . Cos α.
Diferença entre grandezas vetoriais e escalares
Vamos supor que alguém te disse que vai chegar em sua casa às 5h30min, ou que alguém disse que a temperatura da cidade está hoje em 31°C. Você, sem dúvidas, irá entender as frases sem mais nenhuma informação adicional, pois são grandezas escalares. Área, volume, massa e energia também são grandezas escalares.
Porém, se um barco desloca 5km, para onde ele irá? Não sabemos a posição final do barco, pois ele pode ir para qualquer direção, só podemos determinar essa posição final se soubermos a direção e o sentido do deslocamento.
Grandezas que precisam de indicação de direção e sentido onde atuam são conhecidas como grandezas vetoriais, como o deslocamento, a força, a velocidade, a aceleração e o campo elétrico.
Exercício resolvido
1) Na figura abaixo, estão representadas duas forças de módulo F1 = 5 N e F2 = 3 N, formando entre si um ângulo α = 60°.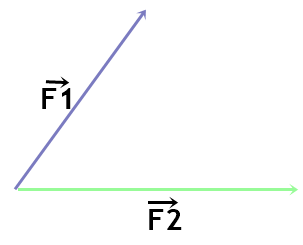
Determine o módulo F da força resultante dessas duas forças. Dado cos 60° = 0,5
RESOLUÇÃO:
Aplicando a regra do paralelogramo:
F² = F1² + F2² + 2F1.F2 . Cos α
F² = 5² + 3² + 2 . 5 . 3 . 0,5
F² = 25 + 9 + 30 . 0,5
F² = 49
F = 7 N
