Oscilações são movimentos que se repetem e estão presentes em várias situações do nosso cotidiano, como nas cordas de um violão, nos diafragmas em telefones e nos sistemas de alto-falante. Porém, as oscilações do mundo real são amortecidas: o movimento vai diminuindo gradativamente até desaparecer. Porém, podemos reabastecer a energia por meio de alguma fonte que mantenha ou aumente essas oscilações.
Movimento periódico ou movimento harmônico é qualquer movimento que se repete em intervalos regulares. Uma propriedade importante do movimento oscilatório é sua frequência, que é o número de oscilações completas a cada segundo. O símbolo da frequência é f e sua unidade no SI é o hertz (abreviado por Hz), sendo
- 1 hertz = 1 Hz = 1 oscilação por segundo = 1 s-1.
O período T do movimento é o tempo necessário para uma oscilação completa (1 oscilação completa é chamada de ciclo), ou seja: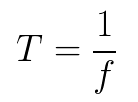
Moimento harmônico simples (MHS)
Existem vários movimentos oscilatórios, porém classificamos como movimento harmônico simples (ou oscilação harmônica simples) o movimento oscilatório em que existe relação entre a sua posição e a velocidade do movimento.
Para compreendermos um MHS, podemos relacioná-lo com o movimento circular uniforme (MCU). O movimento circular uniforme descreve o percurso de um ponto em uma trajetória circular.
A massa da mola, em MHS, comporta-se como uma projeção do ponto que se move em MCU, como mostra a imagem abaixo: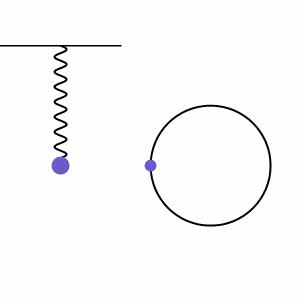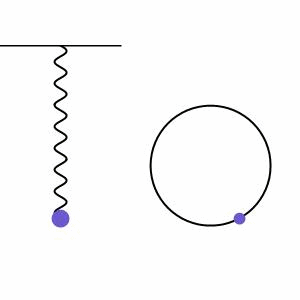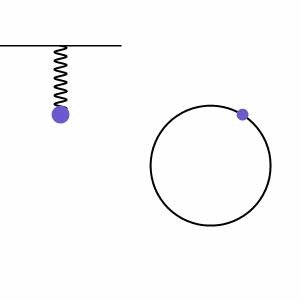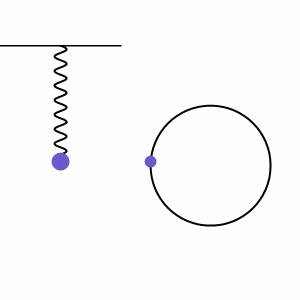
Aqui, podemos ver um corpo em movimento circular uniforme (bolinha preta) com suas projeções nos eixos “x” (bolinha vermelha) e “y” (bolinha verde).
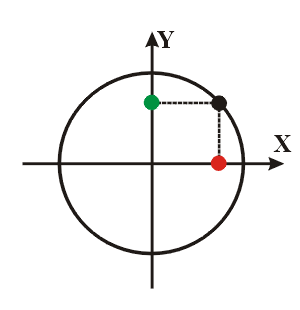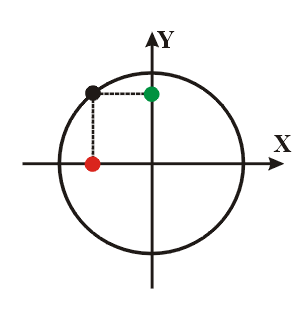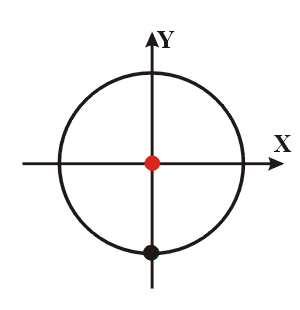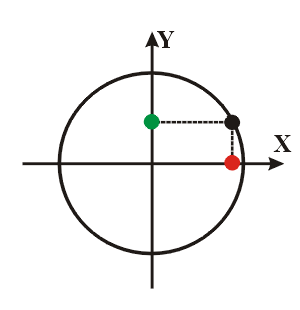Essas projeções são utilizadas para formarmos o MHS. A partícula em movimento circular uniforme percorre a circunferência com velocidade angular ω constante. A projeção dessa partícula no eixo x (bolinha vermelha) descreve um movimento de vai em vem entre dois extremos. Chamamos esses extremos de amplitude A do movimento, que corresponde ao raio do círculo.
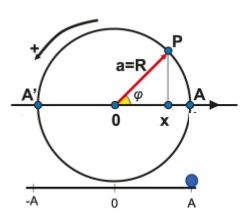
O ângulo que a partícula faz com o eixo x é chamado de ângulo de fase φ. Além disso, no MHS também temos a frequência e o período do movimento.
Chamamos também de elongação o número que indica a posição do ponto vermelho no eixo x.
Observe, na imagem abaixo, um momento no qual a partícula se encontra em determinada posição.
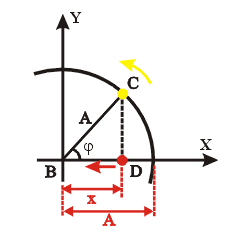
Podemos observar o triângulo BCD e dizer que: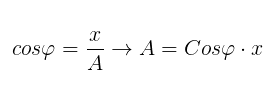
Sabemos que, em MCU, o ângulo de fase é dado por:
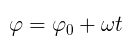Fazendo uma substituição, encontramos a função da elongação em relação ao tempo:
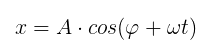A velocidade da partícula em MCU (VMCU) é tangente à trajetória, como mostra a seta em verde da figura abaixo, que representa o vetor VMCU:
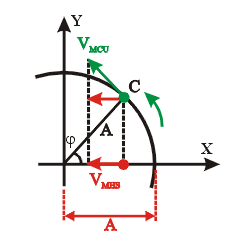
A equação da velocidade no MHS é dada por: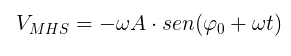
A aceleração centrípeta no MCU é perpendicular à velocidade e sempre em direção ao raio da circunferência que forma o movimento, ou seja, sempre em direção ao centro, como mostra a seta em azul escuro (que representa o vetor aceleração), na figura abaixo: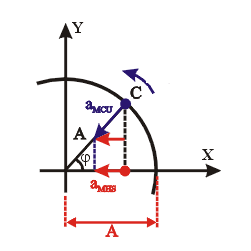
A aceleração do MHS é dada por: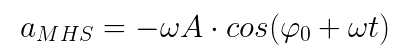
Ela também pode ser dada por: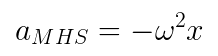
Dinâmica do movimento harmônico simples
O movimento de um pêndulo não-amortecido e um sistema de massa-mola não-amortecida são exemplos de situações nas quais encontramos movimentos harmônicos simples.
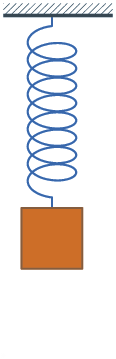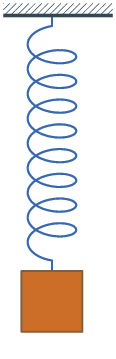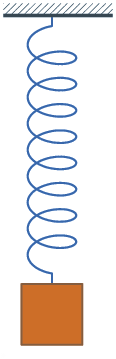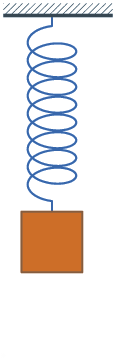
Nos dois casos, há uma posição chamada de posição de equilíbrio. Nela, podemos verificar que o movimento é igual (em módulo) para lados opostos, ou seja, é um movimento simétrico.
Dois fatores são necessários para que haja oscilação mecânica nesses dois casos:
- A existência de uma força restauradora, que age sempre para levar o corpo de volta à posição de equilíbrio; a força da gravidade no caso do pêndulo, e a elasticidade, no caso da mola;
- A inércia, que é a tendência dos corpos em movimento se manterem em movimento.
Sistema massa-mola: temos um sistema massa mola quando um corpo preso à extremidade de uma mola previamente fixada a um suporte obedece à Lei de Hooke.
As equações utilizadas para resolver exercícios que apresentam um sistema massa-mola são:
Pendulo Simples: o pêndulo simples é constituído por um fio ideal fixado verticalmente e por um corpo preso em sua extremidade.
As equações utilizadas para resolver exercícios que apresentam um pêndulo simples são:
Funções horárias do movimento harmônico simples
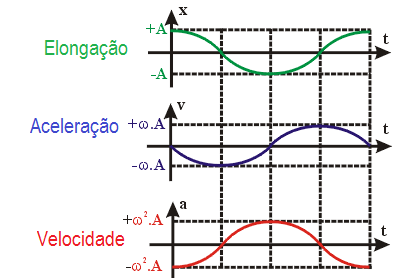
Como toda função, podemos obter uma representação gráfica das funções horárias do movimento harmônico simples.
Desse modo, a representação gráfica da velocidade, aceleração e elongação no MHS é dada por: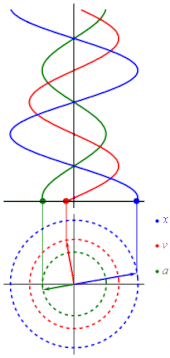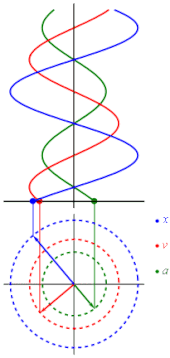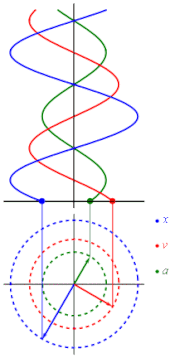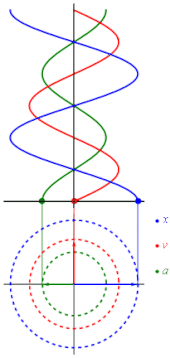
Gerando os gráficos:
