Identidade trigonométrica é toda igualdade envolvendo funções trigonométricas que é verdadeira para todos os valores do domínio dessas funções, isto é, independentemente de qualquer contexto e dos valores assumidos por suas variáveis.
Elas representam um caso geral e podem resultar em uma propriedade ou um princípio, servindo para identificar a igualdade da função apresentada na direita com a função mostrada na esquerda. Usamos isso em processos em que queremos realizar a substituição de uma função trigonométrica ou parte de uma expressão para facilitar os cálculos, portando essas identidades serão aplicadas nas equações trigonométricas.
Na Grécia Antiga, surgiram algumas identidades trigonométricas que já eram usadas, porém expressas em corda. Principalmente nos séculos V a XII, matemáticos hindus estabeleceram as fórmulas que conhecemos hoje por relações trigonométricas.
As relações surgem uma a partir das outras por raciocínio dedutivo, sendo que a principal relação trigonométrica (sen² a + cos² a = 1) teve origem com o Teorema de Pitágoras.
Relações fundamentais
Além de seno, cosseno e tangente, existem outras três funções trigonométricas importantes por seu valor histórico: secante, cossecante e cotangente.
As relações entre os valores das funções trigonométricas de um mesmo arco são denominadas relações trigonométricas. Observe o círculo trigonométrico de raio igual a 1:
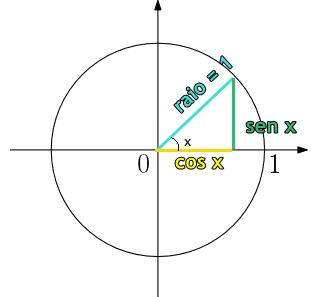
Ao criar um triângulo retângulo em seu centro, temos que a hipotenusa é exatamente o raio do círculo e os dois catetos são os valores de seno e cosseno do ângulo x.
Pelo teorema de Pitágoras, temos que para todo x real, x ∈ [0, 2π], vale:
- Sen2x . cos2x = 1, para todo X ∈ R.
Essa é umas das relações fundamentais.
Ainda no círculo trigonométrico, vamos traçar uma reta tangente a ele no ponto S, que é a reta em vermelho na figura abaixo.
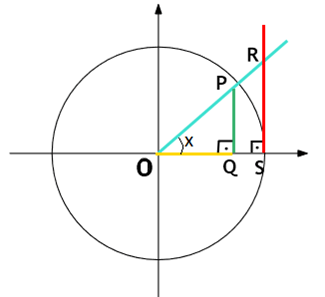
Os triângulos ΔOPQ e ΔORS possuem dois ângulos correspondentes congruentes. Portanto, são triângulos semelhantes.
Por semelhança, podemos dizer que:
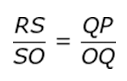
Sendo OQ = cos x e QP = sen x, temos:
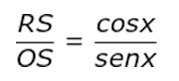
Sendo RS = tg x e OS = 1 (pois OS é exatamente o raio do círculo), temos:
Essa é a segunda relação fundamental.
Existem outras relações fundamentais, que são:
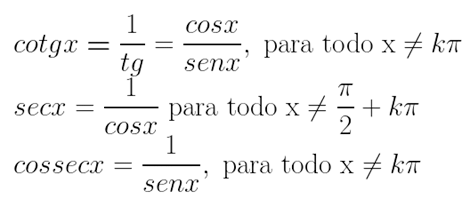
A partir das relações fundamentais, podemos chegar a outras relações também importantes. Para todo x real, x ∈ [0, 2π] e x ∉ [0, π/2, π, 3π/2, 2π], vale as cinco relações que serão demostradas a seguir: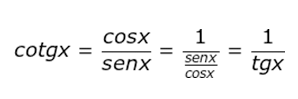
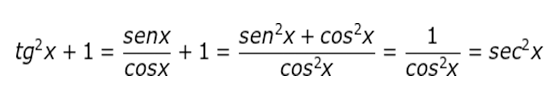
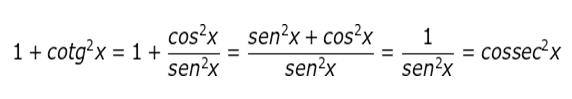
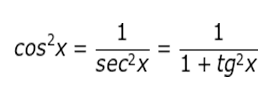
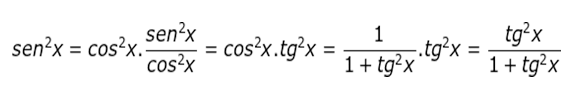
O que são identidades trigonométricas?
Toda igualdade que envolve funções trigonométricas verificada para todos os valores do domínio dessas funções é uma identidade trigonométrica. As relações trigonométricas vistas anteriormente também são identidades trigonométrica.
Por exemplo, considerando o domínio das funções, a igualdade sen x . sec x = tg x é uma identidade trigonométrica, pois, independentemente do valor de x, ela se verifica. Segue a demonstração:
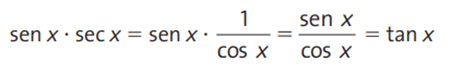
Portanto: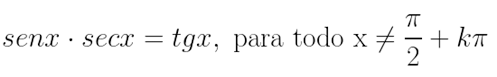
Porém, a igualdade sen x + cos x = 1, com x ∈ R não é uma identidade, pois ela não é verdadeira para todo x ∈ R. Dizemos que sen x + cos x = 1 é uma equação trigonométrica.
Para demonstrar que uma igualdade é uma identidade, existem alguns caminhos. Observe os exercícios resolvidos a seguir.
Exercícios resolvidos
1) Demonstre que (1 – cos² x)(cotg² x +1) = 1, para x ≠ kπ, é uma identidade.
Resolução:
Consideramos que o primeiro membro da igualdade é f(x) e o segundo membro é g(x) e procuramos simplificar o primeiro membro.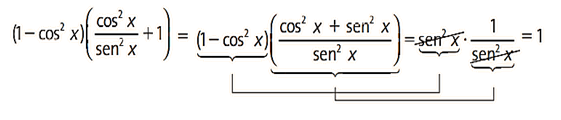
Isto é, partindo de f(x), chegamos a g(x), logo f(x) = g(x). Esse é um dos métodos de se demonstrar uma identidade trigonométrica: trabalhar de um lado da equação até chegar numa expressão igual ao outro lado.
2) Demonstre que tg x/ 1 + tg² x = sen x/ sec x é uma identidade para x ≠ π/2 + kπ.
Nesse problema, vamos simplificar isoladamente cada membro:
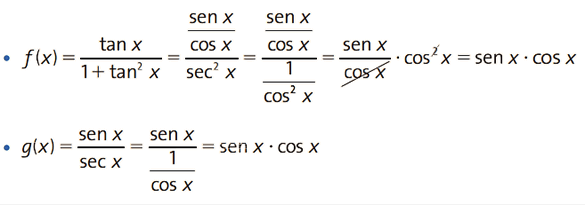
Partindo separadamente de f(x) e g(x), chegamos ao mesmo valor. Logo, f(x) = g(x). Essa é uma segunda maneira de demonstrar identidades trigonométricas.
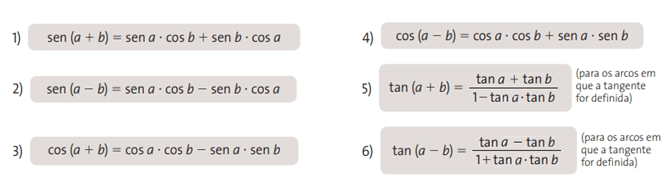
Fórmulas de adição e subtração de arcos
Veremos agora como é possível expressar sen (a ± b) e cos (a ± b) em função de sen a, sen b, cos a e cos b, sendo a e b dois números reais quaisquer.
Veremos também tan (a ± b) em função de tan a e tan b.
