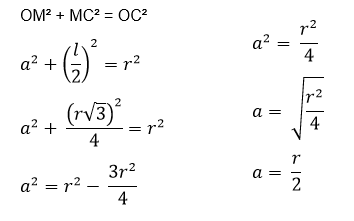As relações métricas nos polígonos regulares estudam como calcular a medida dos lados e a medida do apótema de um polígono regular inscrito em uma circunferência em função da medida do raio.
Se uma circunferência é dividida em três ou mais arcos congruentes (de mesma medida), então as cordas consecutivas formam um polígono regular inscrito na circunferência.
Por exemplo, se em uma circunferência traçarmos dois diâmetros perpendiculares entre si, a circunferência ficará dividida em quatro arcos congruentes.
Ao ligarmos a extremidade dos arcos com cordas, as cordas consecutivas formam um quadrado inscrito na circunferência.
Se um polígono é regular, então existe uma circunferência que passa por todos os seus vértices. Isto é, todo polígono regular pode ser inscrito em uma circunferência.
Elementos de um polígono regular
Um polígono regular possui certos elementos, como:
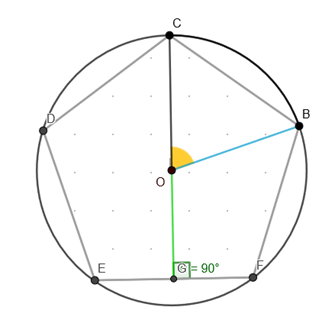
- Centro do polígono: centro da circunferência circunscrita a ele (ponto O);
- Raio do polígono: é o raio da circunferência circunscrita a ele (segmento em azul OB);
- Apótema do polígono: é o segmento que une o centro do polígono ao ponto médio de um de seus lados (segmento em verde OG);
- Ângulo central: é aquele cujo vértice é o centro do polígono e cujos lados são semirretas que contêm dois vértices consecutivos do polígono (ângulo em amarelo).
Relações métricas nos políginos regulares
Quadrado inscrito
Considere uma circunferência de centro O e raio de medida r. Para construir um quadrado ABCD inscrito nessa circunferência, traçamos dois diâmetros perpendiculares entre si, determinando os vértices dos quadrados:
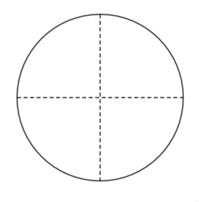
Depois, basta ligar os vértices consecutivos a partir de cordas traçadas. Vamos definir a medida do raio como r, a medida dos lados como l e a medida do apótema como a.
Para calcular a medida l do lado JH, observe o triângulo OJH.
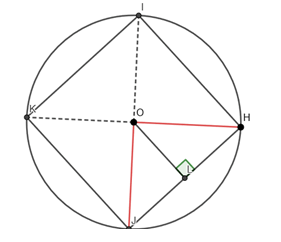
Como os segmentos OH e OJ são os raios que medem r, temos, pelo Teorema de Pitágoras: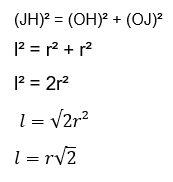
Portanto, o lado do quadrado pode ser calculado por l = r (raiz de 2).
Para calcular a medida do apótema OL de medida a, observe o triângulo OHL da figura:
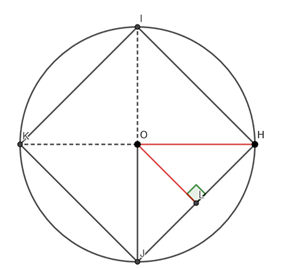
Pelo Teorema de Pitágoras, temos:
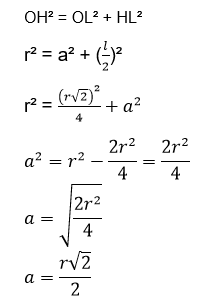
O cálculo por meio de fórmulas é uma maneira de determinar a medida do lado ou do apótema. Mas, também podemos calcular as medidas construindo a figura e aplicando o Teorema de Pitágoras.
Hexágono regular inscrito
Considere uma circunferência de centro O, raio de medida r e apótema de medida a.
Como o ângulo central do hexágono mede 360°/6 = 60°, podemos construir, na circunferência, um ângulo central com esse valor, obtendo um arco AB. Com a abertura de um compasso igual a AB, marcamos os outros vértices do hexágono.
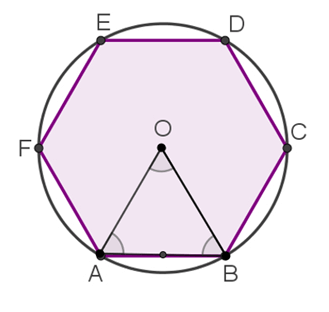
Para o calculo da medida do lado, temos que a medida do ângulo AÔB é igual a 60° – m(AOB) = 60°
Temos que a medida do ângulo ABO é a metade da medida do arco AE.
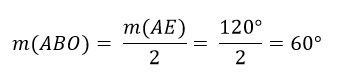
Além disso, a medida do ângulo BAO é igual a metade da medida do arco BD.
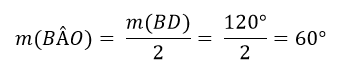
Portanto, todos os ângulos internos do triângulo ABO são iguais a 60°, ou seja, esse triângulo é equilátero. Se o lado OB é o raio da circunferência e mede r, então todos os lados valerão r. Portanto, o lado AB do pentágono mede r, assim como todos os seus lados – l = r.
Para o cálculo da medida do apótema do pentágono, observe o triângulo SOB na figura abaixo:
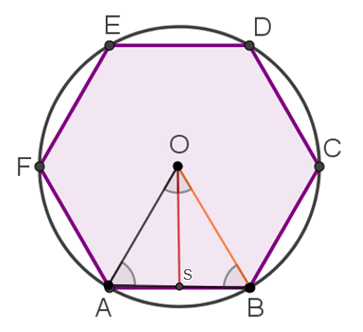
O apótema é o segmento OS que tem medida a.
Aplicando o Teorema de Pitágoras no triângulo SOB, temos:
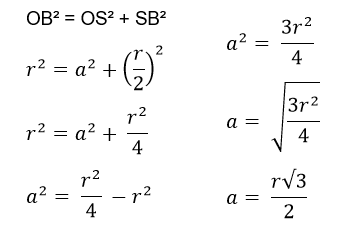
Triângulo equilátero inscrito
Considere uma circunferência de centro O e raio r. Para construir um triângulo equilátero ABC inscrito nessa circunferência, dividimos a circunferência em seis arcos congruentes e, a seguir, unimos alternadamente os pontos de divisão.
Para calcular a medida do lado l, observe que o triângulo VWN:
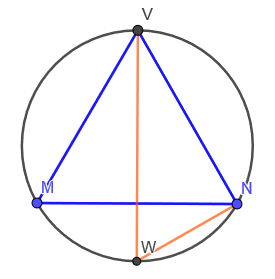
VWN é retângulo, pois está inscrito na semicircunferência. O segmento WN tem medida r igual ao raio.
Pelo Teorema de Pitágoras, temos:
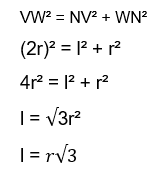
Para o calculo da medida do apótema, aplicaremos o teorema de Pitágoras no triângulo OMC:
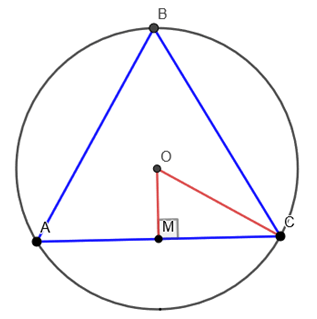
Temos: