É denominada progressão aritmética (PA) toda sequência numérica em que, a partir do segundo termo, a diferença entre cada termo e o termo anterior é uma constante. Essa constante é chamada de Razão da PA, a qual indicamos por r.
Por exemplo, na sequência (1, 3, 5, 7, 9,…), a partir do segundo termo, se subtrairmos um termo ao seu termo anterior, sempre obteremos o mesmo resultado. Tomando a sequência acima como exemplo, veja como funcionaria:
a2 − a1 = 3 − 1 = 2
a3 − a2 = 5 − 3 = 2
a4 − a3 = 7 − 5 = 2
a5 − a4 = 9 − 7 = 2
Observe que, em todas as subtrações, o resultado foi 2. Isso significa que a razão dessa PA é 2, ou seja, r = 2. Da mesma forma, se quisermos encontrar outros termos da sequência, basta adicionarmos 2 ao termo anterior.
Além disso, podemos também ter progressões aritméticas finitas e infinitas. A PA finita é aquela que tem um número determinado de termos, como por exemplo a sequência (3, 7, 11, 15), que tem apenas 4 termos. Já a PA infinita é aquela que tem infinitos termos, como por exemplo a sequência (1, 3, 5, 7, 9, …), em que, após o 9, haverá outros infinitos termos.
Classificação de uma PA
A partir da razão da PA, conseguimos definir se essa progressão é decrescente, constante ou crescente.
PA decrescente
- Se r < 0, a PA é decrescente
Por exemplo, a sequência (10, 4, -2, -8, -14,…) é uma progressão aritmética de razão -6, pois 4 – 10 = -6. Então, r <0, uma vez que -6 < 0. Logo, essa PA é decrescente.
PA constante
- Se r = 0, a PA é constante.
Por exemplo, a sequência (5, 5, 5, 5, ….) é uma progressão aritmética de razão 0, pois 5 – 5 = 0. Então, r = 0. Logo, essa PA é constante.
PA crescente
- Se r > 0, a PA é crescente.
Por exemplo, a sequência (2, 5, 8, 11, 14, …) é uma progressão aritmética de razão 3, pois 11 – 8 = 3. Então, r > 0. Logo, essa PA é crescente.
Propriedades das progressões aritméticas
Dada uma progressão aritmética finita, a soma de dois termos equidistantes é igual à soma dos extremos. Por exemplo, na progressão (2, 5, 8, 11, 14, 17, 20, 23), a soma de dois termos equidistantes, 17 + 8 = 25, é igual à soma dos extremos, 2 + 23 = 25.
Outra propriedade é a soma dos termos. Se a progressão aritmética for finita, podemos calcular a soma de todos os seus termos utilizando a fórmula:
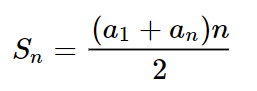
Em que a1 é o primeiro termo da PA, an é o enésimo termo, n é o número de termos e Sn é a soma dos n termos.
Exemplo: na progressão aritmética (2, 5, 8, 11, 14, 17, 20, 23), a1 = 2; an =23; e n = 8.
Assim,
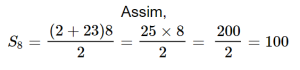
Portanto: Sn = 100.
REFERÊNCIAS
BALESTRI, Rodrigo Dias. Progressão aritmética (PA). MATEMÁTICA Interação e Tecnologia. 2. ed. São Paulo: Leya, 2016. v. 1, cap. 6, p. 183-194.
DANTE, Luiz Roberto. Sequências: Progressão aritmética (PA). MATEMÁTICA Contexto e Aplicações. 3. ed. São Paulo: Ática, 2016. v. 1, cap. 7, p. 213-219.

