Considere a área de um quadrado: lado vezes lado: l2. A área de um cubo, que possui 6 faces, será, então, 6.l2. Agora o volume de um cubo será l3. Repare que, conforme a área cresce com o lado ao quadrado, o volume cresce com l ao cubo.
Se o cubo tiver lado de 2 m, a área total será 6.22=6.4=24 m2. O volume, entretanto, será 23=8 m3.
Se o lado for 8m, a área total será 6.82=6.64=384 m2. O volume será 83=512 m3.
Então temos duas grandezas que se relacionam, mas possuem comportamentos diferentes: o volume cresce mais rápido do que a área. Vamos voltar a esse raciocínio em breve.
Terceira Lei de Kepler

Johannes Kepler percebeu que existe uma relação entre a distância média do planeta ao Sol, que podemos chamar de semieixo maior r, e seu período de revolução T. Essa relação é conhecida como a terceira lei de Kepler:
“O quadrado do período de qualquer planeta é proporcional ao cubo do semieixo maior da órbita”
T2=C.r3
Assim, o período cresce ao quadrado conforme o semieixo maior cresce ao cubo, como na analogia da área e volume.
O valor C é uma constante que possui o mesmo valor para todos os planetas do sistema solar. Assim, podemos escrever C como sendo:
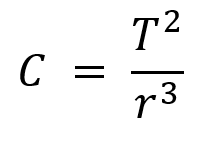
Como C tem o mesmo valor para dois planetas, podemos igualar o C para um planeta a que possui período T1 e distância média r1 com o C de outro planeta b:
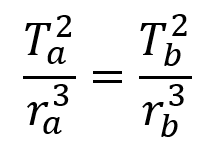
E, assim, podemos comparar os períodos com as distâncias médias. Considere Júpiter como sendo nosso planeta b que possui r valendo 5,2 U.A, período T desconhecido e comparemos com a Terra, nosso planeta a, que possui T de um ano e r de 1 U.A:
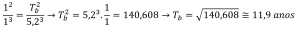
Para um outro sistema planetário ou um conjunto de corpos celestes será feito uso de outra constante C, mas a terceira lei continuará valendo da mesma forma!
Referência
TIPLER, Paul A.; MOSCA, Gene. Physics for scientists and engineers, sixth edition. New York: W. H. Freeman and Company, 2008.
