Potenciação é um número natural que chamamos de base, multiplicado por ele mesmo em uma certa quantidade de vezes, que chamamos de expoente.
As propriedades da potenciação são ferramentas que simplificam operações envolvendo exponenciação. A seguir, vamos estudar essas propriedades e como podemos utilizá-las.
Propriedades da Potenciação
Vamos conhecer abaixo as propriedades da Potenciação:
1 – Multiplicação de potências de mesma base
Para multiplicação de potências de mesma base, devemos manter a base e somar os expoentes.
Exemplo:
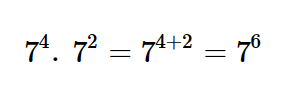
2 – Divisão de potências de mesma base
Para dividirmos potências de mesma base, devemos manter a base e subtrair os expoentes.
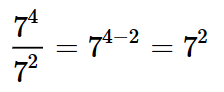
3 – Potência de um produto
Quando multiplicamos dois ou mais fatores e os elevamos a um expoente, podemos separá-los:
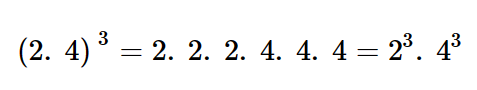
| #Ficaadica!
Embora (2.4)3 seja o mesmo que 23.43, cometeremos um “crime matemático” se afirmarmos que essa regra se aplica para soma de uma potência, já que (2+4)3 não é o mesmo que 23+43. |
4 – Potência de uma divisão
Em uma divisão elevada a um expoente, podemos elevar o numerador e o denominador separadamente.
Exemplo:
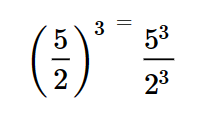
5 – Potenciação de potências
Em uma potência elevada a um expoente, podemos multiplicar os expoentes.
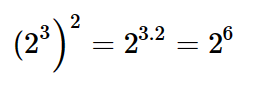
| #Ficaadica!
Embora (23)2 seja o mesmo que 23.2, cometeremos outro “crime matemático” se afirmarmos que 23^2 = 23^2, já que (23)2 = 26 enquanto 23^2 = 29. Lembrem-se: como a vírgula em português, os parênteses na matemática fazem toda a diferença. |
6 – Potências de base negativa
Em uma potência cuja base é negativa e o expoente é:
- par: a potência é positiva.
- ímpar: a potência é negativa.
Exemplos:
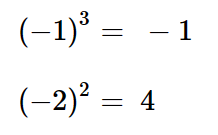
7 – Potências com expoente negativo
Para resolvermos potências com expoente negativo, devemos inverter a base em fração e trocar o sinal do expoente.
Exemplo:
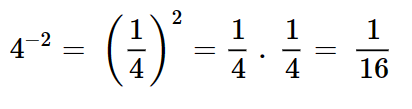
8 – Potências com expoente fracionário
Para resolvermos uma potência com expoente fracionário, devemos transformá-la em raiz, onde o denominador será o índice e o numerador o expoente do radicando, conforme exemplo:
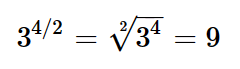
Quando a base da potência é uma raiz, devemos migrar o seu expoente para o radicando, conforme abaixo:
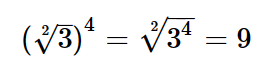
Premissas da potenciação
Além das propriedades, temos definições importantes:
| PREMISSA | EXEMPLO |
| Potência de base 1 é sempre 1. | 1³ = 1. |
| Potência de base 0, é sempre 0. | 0³ =0. |
| Potência elevada a 0 é sempre 1 | 254º = 1 |
| Potência elevada a 1 é sempre ela mesma. | 47¹ = 47 |
Você também pode gostar de ler:
Números Primos – Quais são? Como saber? Tabela completa e Exercícios
Números primos – Quais são? Como saber? Tabela completa e Exercícios

