A fração corresponde a uma parte do todo. Ela determina divisões de partes iguais, sendo que cada uma faz parte de um número inteiro – é a mesma ideia da porcentagem.
O melhor exemplo de fração matemática é pensar numa pizza: a circunferência completa representa o todo, mas ela pode ser dividida em vários pedaços (frações), que fazem parte desse todo. Por exemplo, se essa pizza for dividida em 8 parte iguais, cada fatia corresponderá a 1/8 da pizza; se uma pessoa comer dois pedaços, essa terá consumido 2/8 de piza; e assim por diante.
Para representarmos a fração, utilizamos um número abaixo de outro, sendo o inferior que representa o valor total de alguma coisa e o superior a fração desse total:

O número debaixo da fração se chama denominador, enquanto o número de cima se chama numerador.
Como fazer fração?
Existe uma série de tipos de frações, mas o mais importante é saber como fazer as operações matemáticas básicas usando-as. Aprenda isso, a seguir.

Multiplicação de fração
A forma certa de fazer uma multiplicação fracionária é dividindo os numeradores entre si e os denominadores entre si. Nunca faça de forma cruzada ou misture os números debaixo com os de cima da fração. Confira alguns exemplos na imagem abaixo:
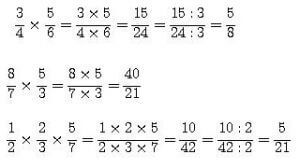
Divisão de fração
Para dividir uma fração, é preciso inverter o denominador com o numerador (o número debaixo com o de cima) e depois multiplicá-los. Observe no exemplo abaixo que o nove muda de lugar com o dois, enquanto que o três muda de lugar com o sete. Depois que é feita a inversão, multiplica-se numerador com numerador e denominador com denominador. Portanto, a divisão da fração 9 por 2, com 7 por 3 é igual a 27/14 avos.
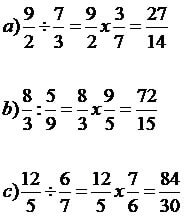
Ficou alguma dúvida? Confira a videoaula sobre divisão de fração:
Soma de fração
Para fazer a adição de duas frações, é preciso somar os numeradores e manter os denominadores, caso eles sejam iguais. Veja como foi solucionado, nos exemplos abaixo:
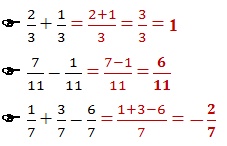
Já a soma de frações com denominadores diferentes implica o uso do Mínimo Múltiplo Comum (MMC), ou seja, o cálculo do menor número de seus denominadores múltiplos de dois. Veja como foi solucionado o caso acima: é tirado o MMC entre 3 e 8 para saber qual será o denominador final. Depois, é feita a soma dos numeradores. O resultado será 6 sobre 21.
Ficou alguma dúvida? Veja a videoaula abaixo:
Subtração de fração
Na subtração de frações, se houver o mesmo denominador comum, basta diminuir numeradores com numeradores e denominadores com denominadores. Já se for denominadores diferentes, será preciso usar o MMC novamente.

No exercício acima, por exemplo, é tirado o MMC de 1 e 4 para descobrir qual será o denominador final, que no caso é 4. Depois disso, deve-se diminuir 2 de 3. O resultado final será -1/4.
Fração equivalente
As frações equivalentes são aquelas que usam números diferentes para mostrar o mesmo resultado. Como exemplo de fração, tanto a fração 2/4 como a 4/8 indicam 1/2. Fica mais fácil quando pensarmos em um exemplo prático, como uma pizza broto de 4 pedaços, que teve dois pedaços comidos (2/4). Ou seja, metade dela foi comida (1/2). O mesmo acontece se a pizza tivesse 8 pedaços e tivessem sido comidos 4: metade dela (1/2) teria sido consumida. Percebe como essas frações significam a mesma coisa?
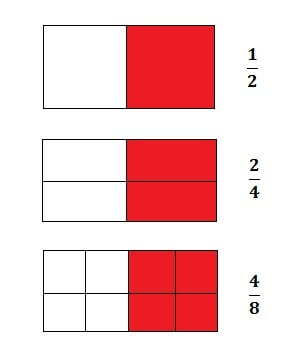
Portanto, em exercícios de frações equivalentes, é preciso prestar atenção em que número é preciso multiplicar ou dividir para obter a mesma representação de quantidade. A fração equivalente de 2/5, por exemplo, é de 4/10, porque a fração inicial é multiplicada por 2.
Tipos de frações
As frações, na matemática, recebem classificações, para orientar o estudante. Os nomes servem somente para dizer de que tipo de solução se trata aquele problema matemático. Confira o que quer dizer cada uma das frações e saiba identificá-las:
Frações próprias
São aquelas em que o numerador é menor que o denominador. Exemplos:1/2, 3/8, 5/8 etc.
Frações Impróprias
Frações em que o numerador é maior ou igual ao denominador. Exemplos: 5/3, 8/2, 6/6 etc.
Frações mistas
São as frações que têm números inteiros, como no caso abaixo:

Frações Aparentes
Quando o numerador da fração é múltiplo do denominador (é divisível), tal como: 9/3,6/2,20,5. Nesses casos, é possível reduzir a fração.
Agora que você já sabe um pouco mais a respeito das frações, que tal testar os seus conhecimentos nos exercícios que preparamos para você? Basta rolar até o final da página e se divertir! Ah, e não deixe de compartilhar com os seus amigos, desafiando eles também.
