O interesse pelas formas geométricas, não se preocupando com as medidas, acompanha os seres humanos até hoje. Vivemos num mundo cercado por formas. Elas estão presentes em tudo o que vemos, na arquitetura das cidades, nas artes e nas coisas do cotidiano. O ser humano, provavelmente, percebe formas desde sempre.
A palavra geometria significa “medida da terra” (geo = terra; metria = medida). Ela está associada ao estudo das formas, tendo origem na questão da medida de propriedades entre os povos antigos.
Nesse estudo, destacaram-se grandes matemáticos, como Pitágoras, Euclides e Arquimedes, que descobriram as fórmulas para desenhar e medir figuras planas, como círculos, esferas e triângulos.

Área de figuras planas
A seguir, você verá alguns aspectos da Geometria, em especial os relacionados às medidas de comprimento e área, utilizando a linguagem algébrica. Em poucas palavras, toda superfície plana ocupa uma extensão do plano, e determinar a área de uma superfície significa medir tal extensão.
Área do retângulo
Retângulo é um quadrilátero que tem todos os ângulos internos retos, lados dois a dois e medidas iguais. Os dois lados não paralelos são perpendiculares entre si.

A área do retângulo é dada por: A = b . h, ou seja, “a área de um retângulo é igual ao produto da medida da base pela medida da altura”.
Área do quadrado
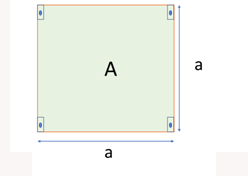
Um quadrado de lado a nada mais é do que um retângulo de base b e altura h. Portanto, na determinação de sua área, vale a fórmula usada para a área do retângulo (A = a * a), ou seja, A = a2. Portanto, “a área do quadrado é igual ao quadrado da medida do lado”.
Área do paralelogramo
O paralelogramo ABCD da figura, abaixo, é equivalente ao retângulo ABEF, pois ΔADF ≡ ΔBCE . Portanto, a área do paralelogramo é obtida da mesma maneira que a área do retângulo.

Ou seja, A = b . h é “a área do paralelogramo igual ao produto da medida da base pela medida da altura”.
Exemplo:
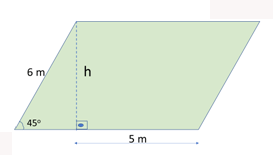
Para determinar a área do paralelogramo, acima, podemos usar a seguinte relação trigonométrica e, primeiramente, determinar o valor de h:
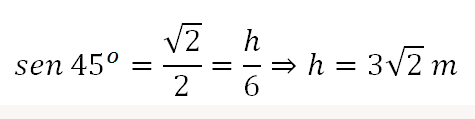
Além disso, como o triângulo é isóscele, (dois lados iguais), temos que a base é dada por b = (5 + h), logo:
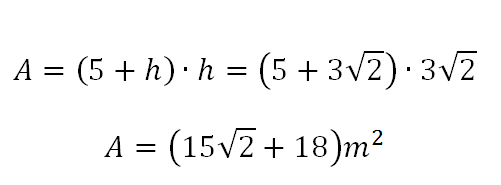
Área do triângulo
O triângulo é uma das figuras mais importantes da Geometria. Eles são utilizados, por exemplo, em construções (telhados, escadas, etc.). Veja o triângulo ABC, de base b e altura h, abaixo:
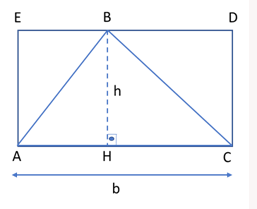
Observe a congruência entre os triângulos ABE e ABH. Como o mesmo ocorre entre os triângulos BCD e BCH, a área do triângulo ABC mede a metade da área do retângulo ACDE.
De modo geral, para um triângulo de base b e altura h – seja ele de que tipo for – podemos escrever:
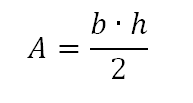
Ou seja, “a área de um triângulo é igual à metade do produto da medida da base pela medida da altura respectiva”.
Área do trapézio
Seja o trapézio MNPO da figura, de bases B e b e altura h. Neste caso, a área dessa figura pode ser dada por:
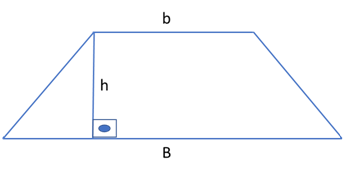
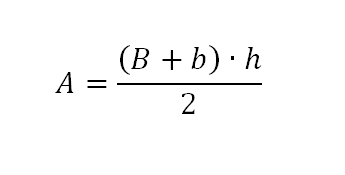
Ou seja, “a área do trapézio é igual à metade do produto da soma das bases pela altura”.
Exemplo:
A área de um trapézio de bases 6dm e 3dm e altura 2dm é dada por:
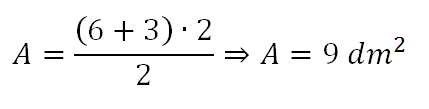
Área do losango
Uma das representações mais famosas do losango está presente na Bandeira Nacional do Brasil. Como o quadrado, o losango tem quatro lados iguais. Entretanto, a diferença é que o quadrado possui quatro ângulos iguais a 90º, enquanto o losango possui dois ângulos agudos (menores que 90º) e dois ângulos obtusos (maiores que 90º).
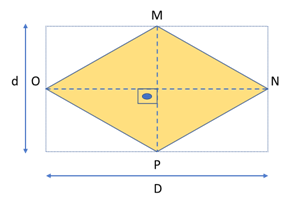
Seja o losango MNPO da figura, de diagonais D e d. Nesse caso, a área é dada por:
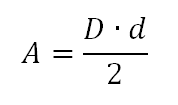
Ou seja, “a área do losango é igual à metade do produto das medidas das diagonais“.
Exemplo:
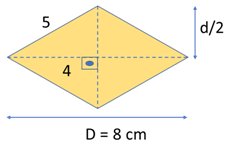
Um losango de lado l = 5cm e diagonal D = 8cm possui a diagonal d dada pelo Teorema de Pitágoras:
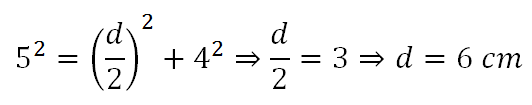
Assim, a área do losango vale
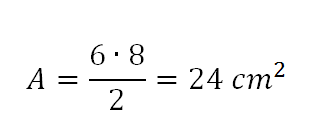
Área do polígono regular
As várias formas encontradas na natureza têm chamado a nossa atenção há muitos séculos. Os favos de mel construídos pelas abelhas, por exemplo, têm o formato de um polígono.
Essa forma geométrica regular é uma figura que tem todos os lados e ângulos iguais, por exemplo: triangulo equilátero, quadrado, pentágono regular, hexágono regular, etc.
Todo polígono regular de n lados de medida l pode ser decomposto em n triângulo de base l e altura a, sendo a o apótema do polígono. Isto é, o segmento que une o centro do polígono ao ponto médio de um dos lados.
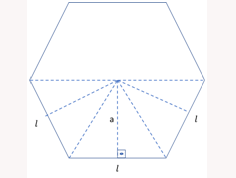
A área do polígono é dada por:
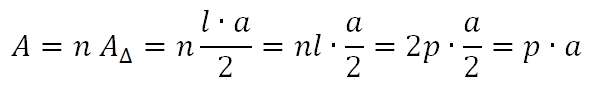
Em geral, A = p . a, ou seja, “a área de um polígono regular é igual ao produto do semiperímetro pelo apótema”.
O semiperímetro (p) é a medida da metade do perímetro de uma figura geométrica. Neste caso,
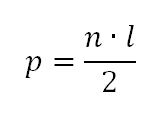
Em que n é o número de triângulos no qual a figura pode ser decomposta.
Exemplo
Na determinação da área de um hexágono regular de lado 8cm, devemos notar que ele pode ser decomposto em seis triângulos equiláteros, como mostra a figura, abaixo.
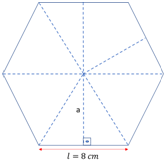
O apótema do hexágono é a própria altura de cada triângulo, portanto:
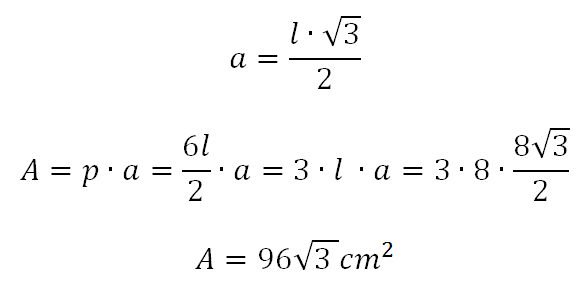
Neste caso, usamos que,
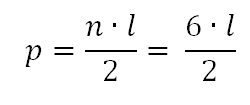
Pois o hexágono tem seis lados, isto é, por ser decomposto em seis triângulos.
Gostou? Então, confira, também, o conteúdo completo sobre Geometria espacial – Características, Figuras e Cálculos!
