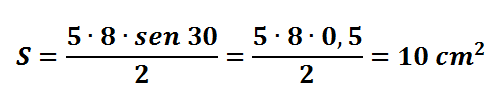O triângulo é um polígono com três lados e três ângulos, estando bastante presente em nosso dia a dia. Uma outra importante propriedade desta figura geométrica é a sua área.
Confira mais, a seguir no Gestão Educacional!
Como calcular a área do triângulo?
Para se ter a noção do cálculo de área do triângulo, considere os triângulos congruentes ABD e CDB, com base de medida b e altura relativa à base de medida h. Justapondo estes dois triângulos, eles formam o paralelogramo ABCD, como mostra a figura.
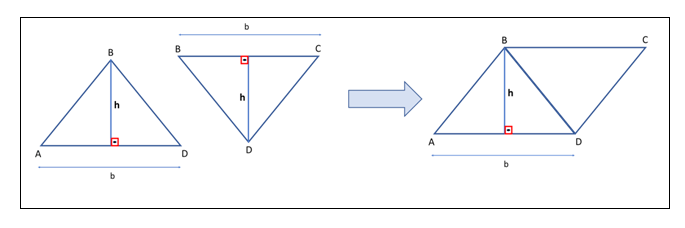
Como os dois triângulos são congruentes, podemos afirmar que a área do triângulo é igual à metade da área do paralelogramo. Portanto, temos que a área de um triângulo é dada por:
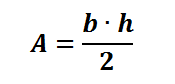
Exercícios resolvidos
Determine a área de um triângulo cuja base mede 25cm e cuja altura mede 12cm.
Para resolver este exercício, basta substituir os valores da base (b =25)e da altura (h = 12) na fórmula acima, como mostra os cálculos a seguir:
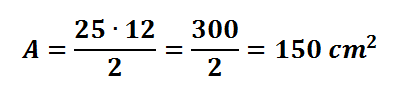
Após esta breve introdução, confira, a seguir, alguns casos particulares da área do triângulo.
Triângulo retângulo
Todo triângulo retângulo, além do ângulo reto, possui dois ângulos (agudos) complementares. O maior dos três lados do triângulo é o oposto ao ângulo reto e chama-se hipotenusa (a); os outros dois lados (b e c) são os catetos, como mostra a figura abaixo.
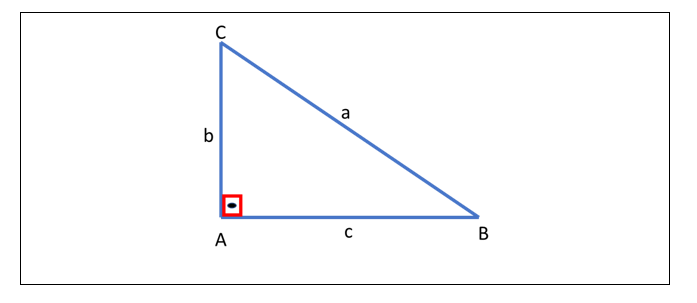
Neste caso, a área da figura geométrica será dada por:
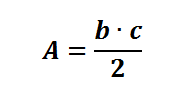
Exercício:
Determinar a área de um triângulo retângulo cujos catetos medem 8m e 10m.
Resolução
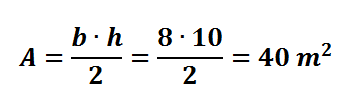
É importante lembrar que o Teorema de Pitágoras é uma ferramenta importante para encontrar o tamanho de um dos lados do triângulo retângulo, conhecendo os outros dois lados.
Aprendemos que em todo triângulo retângulo o quadrado da medida da hipotenusa é igual à soma dos quadrados das medidas dos catetos, ou seja, a2 = b2 + c2.
Triângulo equilátero
Para calcular a área de um triângulo equilátero com lado de medida l, vamos primeiro determinar a medida h da altura CM.
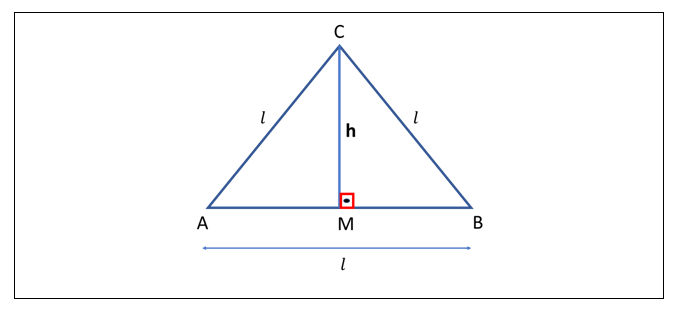
Como o ΔCMB é retângulo, podemos aplicar o Teorema de Pitágoras para determinar o valor de h, ou seja:
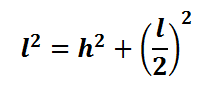
O próximo passo consiste em isolar h:
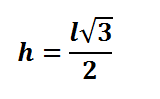
Note que, no triângulo equilátero, a altura relativa a um lado é também mediana e bissetriz. Sabendo que que a área do triângulo equilátero é dada por A = b . h, dividido por 2, e substituindo o valor de h, encontraremos que:
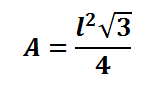
Triângulo circunscrito e inscrito em uma circunferência
Circunscrito
Considere um triângulo ABC circunscrito a uma circunferência de centro O e raio de medida r.
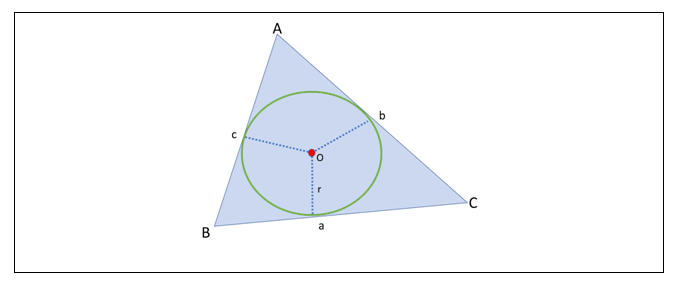
A área de um triângulo circunscrito a uma circunferência com raio de medida r pode ser calculada por A = p.r. Em que p é o semiperímetro do triângulo. Neste caso, temos uma relação entre as medidas do círculo e as do triângulo.
Exercício:
Determine a área do triângulo, sabendo que a= 45cm, b =6cm e c =75cm. Considere que ele esteja circunscrito em uma circunferência de raio igual a 1,5cm.
Resolução
O primeiro passo consiste em determinar o semiperímetro do triângulo.
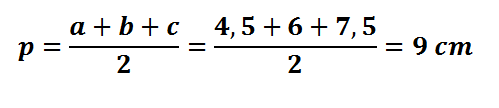
Em seguida, podemos determinar a área como: A = p.r = 9 . 1,5 = 13,5cm2.
Inscrito
Considere, agora, um triângulo ABC inscrito em uma circunferência de centro O e raio de medida R.
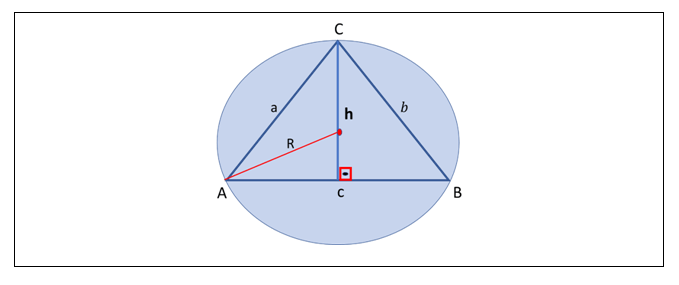
A área de um triângulo inscrito em uma circunferência com raio de medida R é dada por: A = a . b .c, dividido por 4R, em que a, b e c são medidas dos lados do triângulo.
[CONFIRA TAMBÉM: TRIÂNGULO ISÓSCELES]
Formula de Herão
A fórmula de Herão, matemático que viveu a segunda metade do século I d.C., determina a área de um triângulo conhecendo-se apenas as medidas de seus lados. Observe:
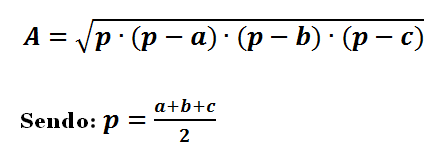
Área de um triângulo qualquer
Há situações em que não são fornecidas as medidas da base e da altura do triângulo. Nestes casos, podemos calcular a área igual ao semiproduto das medidas de dois lados pelo seno do ângulo por eles formado.
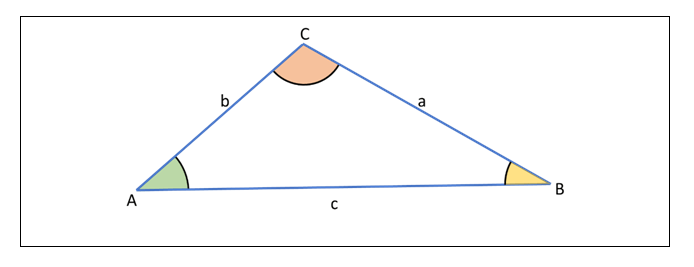
Considere o triangulo ΔABC e S a sua área, podemos obter as seguintes fórmulas:
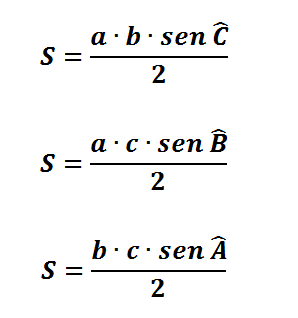
Essa fórmula é válida para um triângulo acutângulo, retângulo e obtusângulo.
[LEIA TAMBÉM: TRIÂNGULO ESCALENO]
Exercício
Qual a área de um triângulo cujas medidas de dois lados são 5cm e 8cm e o ângulo entre eles mede 30º?
Resolução:
Aplicando a fórmula da área de um triângulo qualquer, temos: