Provavelmente, você já notou que os números estão por toda a parte, seja na escola, em casa, na rua, no ônibus, nos esportes, etc. As atividades de contagem que são realizados no dia a dia indicam que nós vivemos em uma sociedade repleta de números. Podemos até mesmo afirmar que não vivemos sem eles.
Dentre a grande quantidade de números, podemos perceber algumas semelhanças entre eles, de modo que algumas características nos permitem formar grupos ou conjuntos de números.
Como exemplo desse agrupamento, confira, a seguir no Gestão Educacional, um pouco mais a respeito dos números naturais!

O que são números naturais?
Os números naturais são aqueles que usamos para contar. Em outros termos, podemos dizer que os números naturais são números inteiros positivos, isto é, não negativos. Eles são frequentemente denotados pelo símbolo .
A representação do conjunto de número naturais é dada por = {0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11 , …}.
Note que essa sequência é infinita. Portanto, não é possível dizer que exista um número inteiro que seja o maior de todos os números naturais.
Entretanto, o mesmo não é possível dizer para o menor, pois, o Zero é considerado o menor dos números naturais.
Podemos representar os números naturais em uma reta numérica, como a ilustrada abaixo:

Nela, o zero é associado à origem (ponto O), e à distância entre os pontos que representam dois números inteiros consecutivos.
Exemplo:
Dos números representados no conjunto a seguir, indique aqueles que são números naturais.
Conjunto = {-3, -1,234 … 0, ½, 1, 2, 3, 4.5}.
Resposta:
Apenas os números 0, 1, 2, 3 são números naturais.
Antecessor e sucessor
Observando a sequência dos números naturais, podemos determinar o antecessor e o sucessor de um número natural. Nesse caso, sabemos que o antecessor de um número, em uma sequência, é o número que vem imediatamente antes dele, e o sucessor é o número que vem imediatamente depois dele.
Exemplo
Determine o sucessor e o antecessor dos seguintes números naturais:
a) 99
b) 999
c) 1000
d) 9009
e) 1000
f) 45
Resposta:
Para responde este exercício, vamos montar a seguinte tabela:
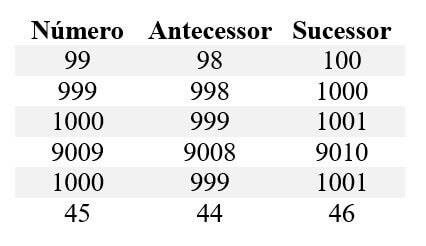
Note que, se x é o sucessor de y, então x é maior do que y. Da mesma maneira, se z é o antecessor de k então, z é menor do que k.
Além disso, observe que, considerando apenas o conjunto de números naturais, o zero não tem antecessor, pois ele é o primeiro número natural. Portanto, pode-se dizer que esse conjunto é limitado.
Números primos
Um número primo é aquele que é divisível apenas por 1 e por si mesmo. Divisível quer dizer que o resultado da divisão é um número inteiro.
Considerando essa propriedade, podemos estabelecer o conjunto dos números primos (P) como um subconjunto dos números naturais, ou seja, P = {2, 3, 5, 7, 11, 13, …}.
Da mesma maneira, o conjunto dos números compostos é formado por todos os números que não são primos. Isto é, P = {4, 6, 8, 10, 12, 14, 15, 16…}.
Número pares e ímpares
Um número par é todo número que, ao ser dividido por dois, resulta em um número inteiro. Por exemplo:
- 4 / 2 = 2 com resto 0 (número par);
- 15 / 2 = 7 com resto 1 (número ímpar).
Para descobrir se um número é par ou impar, pode-se utilizar um método de inferência bem simples. Basta considerar o último digito do número. Se esse for divisível por dois, o número será par, caso contrário, será ímpar.
Exemplo:
- 284 é par, pois o último digito (4) é divisível por 2.
- 45874569 é ímpar, pois o último digito (9) não é divisível por 2.
Exercício
A soma de cinco número ímpares consecutivos é igual a 135. A soma entre o maior e o menor número entre esses cincos é:
(a) 11
(b) 23
(c) 31
(d) 54
(e) 135
Resposta
Em geral, os números pares são representados pela expressão 2n e o números impares por 2n + 1. Assim, a soma dos cinco números impares consecutivos é dada por:
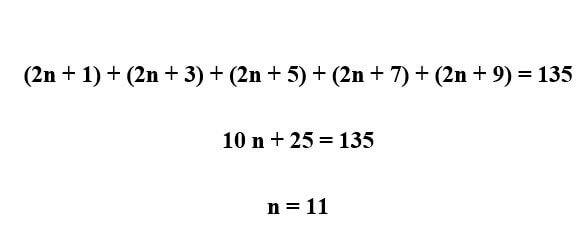
O primeiro número é dado por 2.11+1=23 e o último número é dado por 2.11+9=31. A resposta para o problema é dada pela soma de 23 e 31, ou seja, 54.
A resposta correta é a letra (d).

 .
.