Um dos objetivos da física é explicar as coisas que encontramos em nosso dia a dia. Como já sabemos, nenhum movimento pode ser realizado sem que algum tipo de energia esteja envolvido. Ao levantar uma cadeira, precisamos de energia. Gastamos milhões para obter fontes de energia e mais milhões para pesquisa-las. Mas, afinal, o que é energia?
Iremos definir esses conceitos importantes sobre energia cinética, que é a energia que está relacionada ao movimento dos corpos, aqui, neste artigo do Gestão Educacional!
Esse tipo de energia está diretamente ligado à velocidade do movimento e à massa do corpo que se move, ou seja, qualquer corpo capaz de realizar trabalho possui, portanto, energia.

O que é energia?
A importância de se conceituar o que é energia surge do princípio de conservação de energia. Sabemos que a energia pode ser convertida de uma forma para outra, mas jamais pode ser criada ou destruída.
Em um forno de micro-ondas, por exemplo, a energia eletromagnética obtida da tomada é convertida em energia térmica, que cozinha o alimento. Ou seja, a energia total permanece constante, pois a soma de todas as formas de energia envolvidas também permanece a mesma.
O que é energia cinética?
Vamos considerar uma partícula de massa m movendo-se sob a ação de uma força F.
A aceleração da partícula é constante, dada pela segunda Lei de Newton: F = m.a.
Suponha que, nessa trajetória, a velocidade varie de v1 para v2, enquanto a partícula vai do ponto x1 para x2. Ou seja, ela sofre um deslocamento d = x2 – x1.
Usando a equação do movimento com aceleração constante, podemos obter:
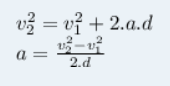
Quando multiplicamos essa equação por m e igualamos a força resultante F com m.a, achamos: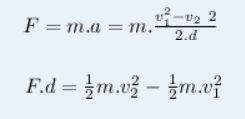
O produto F.d é o trabalho realizado pela força resultante F e, portanto, é o trabalho total W realizado. A grandeza ½ m.v² se denomina energia cinética K da partícula.
Fórmula da energia cinética
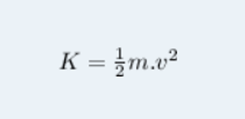
A energia cinética é uma grandeza escalar, portanto, depende somente da massa e do módulo da velocidade da partícula, e não da direção do movimento.
Teorema do trabalho energia
Observe a seguinte fórmula que usamos acima:
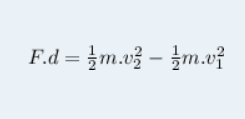
Podemos chamar o primeiro termo dessa equação de K2, que é a energia cinética final da partícula, ou seja, depois do deslocamento:
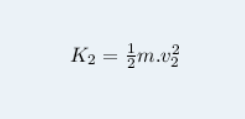
O segundo termo podemos chamar de K1, que é a energia cinética inicial da partícula:
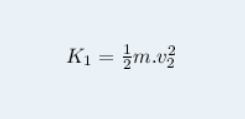
A diferença entre os termos K2 e K1 é a variação da energia cinética. O trabalho realizado pela força resultante sobre a partícula fornece a variação da energia cinética da partícula.
Temos, então, o teorema do Trabalho-Energia:
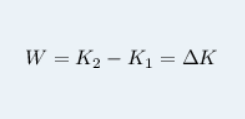
Quando o trabalho W é positivo, a energia cinética aumenta (a energia K2 é maior que a energia K1) e a velocidade final da partícula é maior do que a sua velocidade inicial.
Porém, quando o trabalho W é negativo, a energia cinética diminui (energia K2 menor que energia K1) e a velocidade final da partícula será menor que a velocidade inicial.
Caso seja o trabalho W = 0, a energia cinética é constante (K2 = K1) e a velocidade não se altera.
Tanto o trabalho quanto a energia cinética K possuem a mesma unidade de medida no Sistema Internacional, que é o Joule.
Exercícios Resolvidos
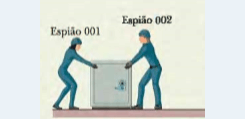
1) A imagem mostra dois espiões industriais arrastando um cofre de 225kg a partir do repouso, assim produzindo um deslocamento d de módulo 8,50m, em direção a um caminhão. O empurrão F1 do espião 001 tem um módulo de 12,0 N e faz um ângulo de 30,0° para baixo com a horizontal; o puxão F2 do espião 002 tem um módulo de 10,0 N e faz um ângulo de 40,0° para cima com a horizontal. Os módulos e orientações das forças não variam quando o cofre se desloca e o atrito entre o cofre e o piso é desprezível.
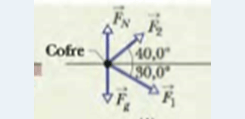
Qual é o trabalho total realizado pelas forças F1 e F2 sobre o cofre durante o deslocamento d? Utilize o diagrama de corpo livre, abaixo.
RESPOSTA: o trabalho total W realizado sobre o cofre é a soma dos trabalhos realizados separadamente pelas duas forças.
Como o cofre pode ser tratado como uma partícula e as forças são constantes, tanto em módulo como em orientação, podemos usar a W = Fd cos (θ) ou W = F · d para calcular esses trabalhos.
Como conhecemos o módulo e a orientação das forças, escolhemos a W = Fd cos (θ).
O trabalho realizado por F1 é W1 = F1 . d. cos θ1 = (12,0 N) . (8,50 m) . ( cos 30,0°) = 88,33 J.
O trabalho realizado por F2 é W2 = F2 . d . cos θ2 = (10,0 N) . (8,50 m) . ( cos 40,0°) = 65,11 J.
Assim, o trabalho total W é W = W1 + W2 = 88,33 J + 65,11 J = 153,4 J = 153J.
Durante o deslocamento de 8,50 m, portanto, os espiões transferem 153J para a energia cinética do cofre.
2) O trabalho total executado sobre uma partícula é de 1300J. Sabendo que a energia cinética antes da execução do trabalho era de 400J, determine o valor da energia cinética depois da execução do trabalho.
RESPOSTA:
Pelo teorema Trabalho-Energia, temos:
W = ΔK
Se o trabalho total executado foi de 1300J, teremos:
1300 J = ΔK
Sendo ΔK = K2 – K1, e K1 = 400J, podemos calcular k2 (energia cinética depois da execução do trabalho) da seguinte forma:
ΔK = K2 – K1
1 300 = K1 – 400
K1 = 1 300 – 400 = 900J
