Na análise combinatória, estudamos como formar grupos com um número finito de elementos, considerando situações preestabelecidas.
Esse tipo de análise possibilitou o avanço da criptografia e, atualmente, informações codificadas chamadas de textos cifrados são empregadas em cartões de crédito, ligações telefônicas e também na internet que você está usando para ler este artigo!
Confira com funciona a análise combinatória, alguns exemplos práticos e exercícios resolvidos sobre o assunto, só aqui no Gestão Educacional!

Princípio fundamental da contagem
Utilizamos, nesse caso, a árvore de possibilidades, também chamada de diagrama de árvore. Para entendermos, vamos pensar no seguinte exemplo:
Se jogarmos um dado e uma moeda ao mesmo tempo, quais serão as possibilidades de resultado?
Ao jogar uma moeda, o resultado pode ser cara ou coroa. Ao jogar um dado, como ele possui 6 faces, temos, então, 6 resultados diferentes possíveis.
A moeda pode cair em CARA e, com isso, o dado pode resultar em 6 faces diferentes. Além disso, a moeda pode cair em COROA e o dado, em seguida, mostrar um de seus 6 resultados diferentes, como mostra o diagrama abaixo:
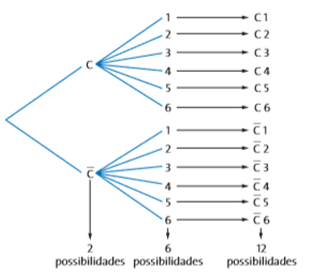
Para encontrar o resultado sem construir o esquema acima, podemos fazer a multiplicação do número de possibilidades: 2 possibilidades da moeda multiplicadas pelas 6 possibilidades do dado – 2×6 = 12 possibilidades ao todo.
Se um evento é composto de duas etapas sucessivas e independentes, sendo o número de possibilidades na 1ª etapa igual a m e, para cada possibilidade da 1ª etapa, o número de possibilidades na 2ª etapa é n, então o número total de possibilidades de o evento ocorrer é dado pelo produto m.n.
Permutação simples e fatorial de um número
Quando tratamos de permutação, devemos associar isso à troca de ordem dos itens, ou seja, embaralhar os itens citados no exercício.
Por exemplo: quantos números de 3 algarismos (sem repeti-los num mesmo número) podemos formar com os algarismos 1, 2 e 3?
123, 132, 213, 231, 312, 321. Ou seja: 3x2x1 = 6 possibilidades.
Se temos n elementos distintos, podemos calcular o número de agrupamentos possíveis que podemos formar com esses elementos utilizando a permutação simples.
Com n elementos distintos, indicamos por Pn o número de permutações simples de n elementos:
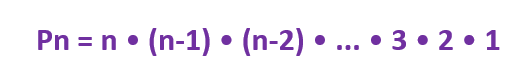
O número Pn é também chamado de fatorial do número natural n e é indicado por n! (leia n fatorial). Portanto:
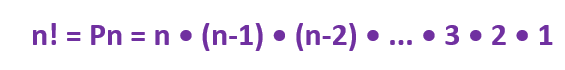
DICAS:
Considere 0! = 1
Anagramas serão calculados utilizando as fórmulas acima. Lembre-se: podemos escrever n! = n. (n-1).
Permutação com repetição
Se quisermos calcular quantos são os anagramas da palavra BATATA, devemos utilizar a formula de permutação com repetição, pois a letra A se repete 3 vezes na palavra e a letra T duas vezes. Faremos, portanto:
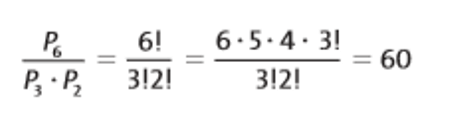
Para isso, usamos, então, a fórmula:
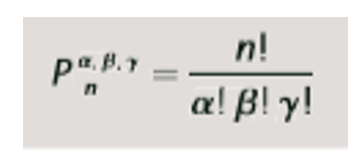
Sendo α, β e γ os fatoriais dos elementos que se repetem, como foi mostrado no exemplo acima.
Arranjo simples
Quando queremos embaralhar n elementos em grupos em que todos esses n elementos são usados, utilizamos a permutação. Porém, se temos n elementos e queremos organiza-los em grupos com quantidades de elementos menores de n, utilizamos a fórmula de arranjo.
Sendo n o número total de elementos e p o número de elementos que vão estar no agrupamento, a fórmula de arranjo será:
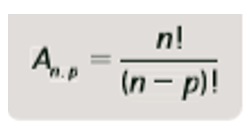
No arranjo, a ordem que os elementos estão é importante, então podemos ainda resolver os exercícios utilizando lacunas para preencher em cada uma o número de possibilidades, como vamos fazer no exemplo abaixo:
Usando os algarismos 2, 3, 5, 7 e 9, quantos números naturais de 3 algarismos distintos podemos formar?

Há 5 possibilidades para o primeiro algarismo, 4 para o segundo e 3 para o terceiro.
A5,3 = 5 . 4 . 3 = 60
Combinação simples
Vamos pensar no seguinte exemplo:
Ana, Elisa, Bruno, Beatriz e Diego precisam fazer uma apresentação, na qual dois deles irão falar em público. De quantos modos podemos organizar esses cinco alunos em grupos de duas pessoas?
Podemos fazer a combinação dessas 5 pessoas em grupos de 2 com a fórmula de combinação de n elementos em grupos com p elementos:

Resolvendo o exemplo, temos: C5,2 = 5! / 2!.(5-2)! = 10 possibilidades.
Perceba que no caso da combinação, a ordem dos elementos não importa, pois é igual um grupo Ana/Elisa e Elisa/Ana.
Exercícios Resolvidos
1) Calcule quantos são os anagramas:
a) da palavra PERDÃO.
b) da palavra PERDÃO, que iniciam com P e terminam em O.
_______________
_______________
_______________
2) Em um plano, marcamos 6 pontos distintos, dos quais 3 nunca estão em linha reta. Quantos segmentos de reta podemos traçar ligando-os 2 a 2?
_______________
_______________
_______________
RESPOSTA:
1.
a) Basta calcular P6 = 6! = 6 . 5 . 4 . 3 . 2 . 1 = 720
b) Vamos utilizar lacunas _ para representar um espaço que será preenchido pelas letras da palavra. Iniciado com P e terminando com O, teremos:
P _ _ _ _ O
Devemos permutar as 4 letras não fixas, ou seja, calcular P4
P4 = 4 . 3 . 2 . 1 = 24
Portanto, há 24 anagramas da palavra PERDÃO iniciados com P e terminados em O.
2.
Marcamos 6 pontos em um plano, no qual não existem 3 alinhados.
Como em cada segmento temos 2 extremos e, por exemplo, o segmento AD é o mesmo que o segmento DA, o número de segmentos é C6,2 = (6.5)/2 = 15.
Portanto, podemos traçar 15 segmentos de reta.
