Círculos são figuras que não possuem lados ou vértices. Eles são, basicamente, o conjunto de pontos inteiros de uma circunferência.
A seguir, vamos descobrir maneiras de calcular a área de uma circunferência só aqui no Gestão Educacional!
Cálculo aproximado da área do circulo
Vamos considerar um círculo com raio de medida r qualquer. Agora, colocamos esse círculo inscrito em um quadrado. Ou seja, como mostra a imagem, vamos colocar o círculo ‘’dentro’’ desse quadrado.
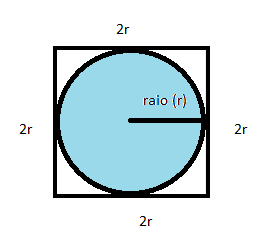
A medida dos lados desse quadrado é duas vezes a medida do raio da circunferência, ou seja, 2r.
Calculando a área desse quadrado, teremos: A = 2r x 2r = 4r².
Portanto, sabemos que a área da circunferência é menor que 4r², pois ela está dentro do quadrado que possui esse valor de área.
Agora, vamos imaginar outra situação: um quadrado inscrito em uma circunferência.
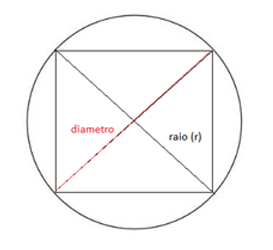
O quadrado tem diagonais da medida do diâmetro (em vermelho), que é equivalente a duas vezes o raio.
Como o quadrado é um caso particular de losango, a área da região quadrada pode ser obtida por: A = (2r . 2r) / 2 = 2r².
Portanto, a área do círculo de raio e é maior que 2r². Com isso, podemos observar que a área de uma circunferência está entre 2r² e 4r², mas não sabemos o seu valor exato por enquanto. Vamos descobrir isso adiante.
Área da circunferência
Para entendermos a seguinte construção, saiba que o comprimento de uma circunferência mede 2.r.π
Podemos dividir um círculo em vários setores. Dividindo o círculo abaixo em um número par de setores, observados que eles adquirem a forma parecida com a de um paralelogramo. Sua base mede metade do comprimento da circunferência, que é π.r, e sua altura mede r, como mostra a figura abaixo:
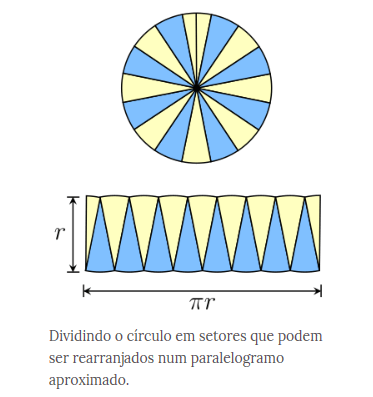
A área do paralelogramo e, consequentemente, a área do círculo será: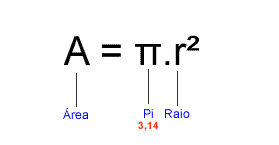
O número π é aproximadamente 3,14. Portanto, anteriormente, ao imaginarmos que o valor da área de uma circunferência estava entre 2 π² e 4 π², estávamos certos! O valor 3,14 está entre o intervalo de 3 a 4.
Exercícios Resolvidos
1) Calcule o valor aproximado da forma plana indicada abaixo:
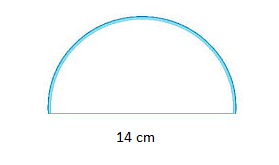RESPOSTA:
Calculando a área de uma circunferência completa, teremos:
Diâmetro: 14cm
Raio: diâmetro/2 = 14/2 = 7 cm
A = r².π
A = 7²π
A = 49π
Como temos uma representação de apenas metade de uma circunferência, vamos dividir por 2 esse valor: A = 49 π/2 = 24,5 π cm.
2) Calcule a área pintada da figura abaixo:
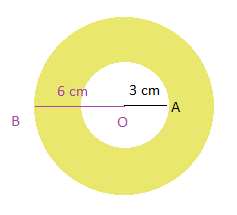RESPOSTA:
O seguimento AO mede 3cm. A área do círculo interno branco será, portanto:
A1 = 3². π = 9 π cm².
O seguimento BO mede 6cm. A área do círculo maior irá medir, portanto:
A2 = 6². π = 36 π cm².
Para calcular a área em amarelo, basta fazer A2 – A1, ou seja, A = A2 – A1 = (36 – 9) π = 27 π.
