Toda a potência escrita na forma (x + y)n com x ∈ R, y ∈ R e n ∈ N é conhecida como Binômio de Newton.
A potência de uma soma até o grau 3 é estudada em produtos notáveis, portanto, são casos mais simples: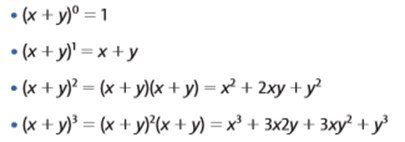
Porém, existem outras situações nas quais o expoente é maior que 3, como em (x + 2)5. Nesses casos, vamos usar o Binômio de Newton e conhecimentos de análise combinatória para resolver exercícios. Para isso, vamos precisar de conhecimentos em número binomial e triângulo de Pascal.
O que é um número binomial?
Chama-se número binomial o seguinte número, com n e p naturais: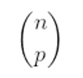
O número binomial de ordem n e classe p é dado por:
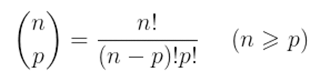Perceba que essa é exatamente a fórmula que usamos para calcular a combinação simples de n elementos em agrupamentos de p elementos (leia “binomial de n sobre p”).
Propriedades dos números binomiais
Binomiais são complementares sempre que p + q = n. Esses binomiais sempre irão resultar em um mesmo valor. Portanto, a igualdade de binomiais ocorre nos dois casos abaixo: se p = q ou p + q = n (binomiais complementares).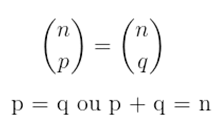
Existem alguns binomiais que não precisamos calcular sempre, pois, como consequência da definição, seus resultados são simples:
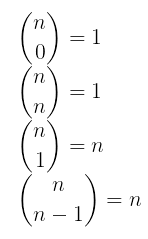Além disso, temos a relação de Stifel, que diz:
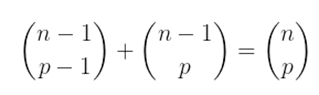Observe, abaixo, alguns exemplos: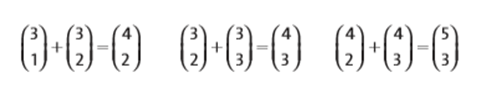
O que é o triângulo de Pascal?
Os números binomiais compõem o triângulo de Pascal, que é infinito e inicia no zero. Os números binomiais do triângulo são formados por: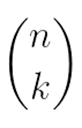
Sendo n o número de linhas e k o número de colunas:
Podemos, então, construir o triângulo de Pascal da seguinte maneira:
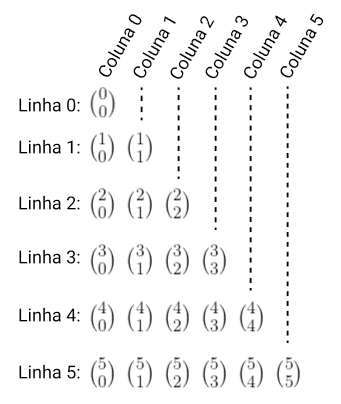Obtendo, enfim:
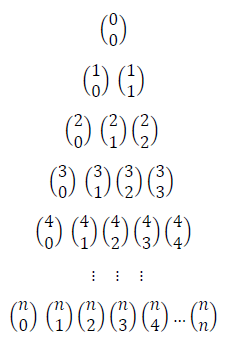Calculando cada um desses números binomiais pela fórmula que vimos acima, chegamos à seguinte formação:
Esse triângulo possui algumas propriedades, que serão discutidas a seguir:
- Todos os elementos da coluna 0 são iguais a 1;
- O primeiro e o último elemento de cada linha são iguais a 1;
- Relação de Stifel: o resultado da soma de dois números sempre estará abaixo deles, como mostra os exemplos: 1 + 3 = 4;
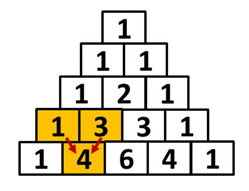
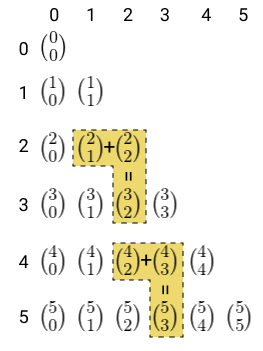
- A soma dos elementos de uma linha será sempre uma potência de base 2 e o seu expoente é o número da linha, portanto, a soma da linha n é 2n.
Binômio de Newton
Observe a expansão do binômio (2 + x)3: (2 + x)3 = 1 .x3.20 + 3 .x2.21 + 3 .x1.22 + 1 .x0.23
Os coeficientes binomiais são os números em negrito: 1,3, 3, 1. Perceba que eles são exatamente os números da linha três do triângulo de Pascal;
Portanto, para descobrir os coeficientes binomiais da expansão do binômio, recorra ao triângulo de Pascal. Caso o expoente do binômio seja um número n, (x + y)n, os números presentes na linha n do triângulo serão os coeficientes da expansão.
Como nós vimos anteriormente que cada número do triângulo de Pascal é obtido por um número binomial, podemos escrever cada coeficiente da expansão do binômio como um número binomial.
Portanto, a fórmula geral do Binômio de Newton para expoente n é dada por: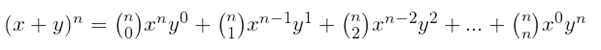
Observe, nos exemplos seguintes, os binômios de Newton desenvolvidos e veja como são cos coeficientes de cada termo:
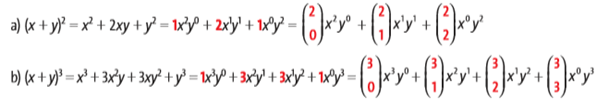Os coeficientes de cada um são as linhas 2 e 3 do triângulo de Pascal.
Note que os expoentes de x começam em n e decrescem de 1 em 1 até 0, enquanto os expoentes de y começam em 0 e crescem de 1 em 1 até n.
Por exemplo: (x + y)² = 1x²y0 + 2x¹y¹ + 1x0y².
Os expoentes de x começam em 2 e decrescem até 0. Enquanto isso, os expoentes de y começam em 0 e crescem até 2.
Além disso, os expoentes de um mesmo termo, quando somados, resultam no número do expoente do binômio. No exemplo acima, no termo 1x²y0 podemos observar que 2 + 0 = 2. Nos termos seguintes, 2x¹y¹ e 1x0y², podemos ver que 1 + 1 = 2 e 0 + 2 = 2, o mesmo valor do expoente 2 de (x + y)².
Para entender melhor sobre o desenvolvimento do binômio de Newton, confira o seguinte vídeo:
Exercício resolvido
1) Efetue o desenvolvimento de (x + a)5
RESOLUÇÃO
Sabemos que os coeficientes são os números da quinta linha da pirâmide de Pascal. Usando a fórmula geral, temos: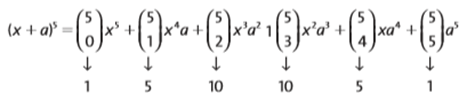
Portanto, o resultado será:
Termo geral do Binômio de Newton
A quantidade de termos de um binômio sempre será o número do seu expoente somado 1. No exemplo acima, em que o expoente é 5, temos, portanto, 6 termos.
Além disso, podemos descobrir qual é o termo independente, o termo médio e o termo em um determinado expoente de x. Para descobrir isso, basta assistir novamente ao vídeo mencionado.
