Definimos bissetriz como a semirreta que parte do vértice do ângulo e o divide em dois ângulos de mesma medida.
Dentre as diversas construções geométricas que temos, esse conceito se torna importante por ser uma das bases para encontrar outras importantes construções.
O conceito de bissetriz é emprestado da geometria e será importante no estudo de funções inversas, como a relação existente entre as funções exponenciais e as logarítmicas.
Construção da bissetriz de um ângulo
Faremos, a seguir, o passo a passo da construção de uma bissetriz.
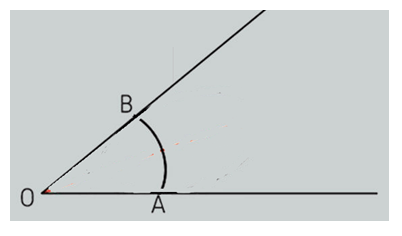
Primeiro, trace um ângulo de vértice O. Para isso, desenhe duas semirretas que irão se unir em um único ponto, o ponto O.
Faça um traço de circunferência sobre as semirretas, com um compasso, colocando a ponta seca no vértice O do ângulo e fazendo um traço de circunferência sobre as semirretas. O compasso pode ter uma abertura qualquer.
Os pontos em que o traço de circunferência cruza as duas semirretas serão chamados de A e B, como mostra a figura abaixo.
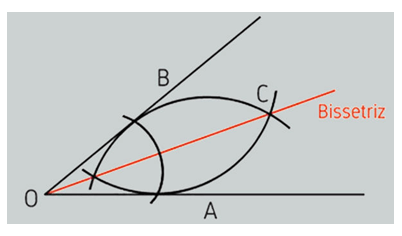
Após isso, com essa mesma abertura, coloque a ponta seca do compasso no ponto A e faça o segundo traço de circunferência. Repita o processo, mas agora com a ponta seca no ponto B.
O ponto de intersecção dos dois novos traços de circunferência será o ponto C.
Por fim, ligue o ponto O ao ponto C. Finalmente, terá a semirreta OC que é a bissetriz desse ângulo.
Bissetriz de um triângulo
Primeiro, vamos definir o que são ângulos congruentes. Dizemos que dois ângulos são congruentes quando têm a mesma medida.
Observe o triângulo ABC, com o ponto S pertencente ao lado BC. O seguimento AS divide o ângulo  em dois ângulos congruentes, ou seja, BÂS = CÂS
O seguimento AS é uma bissetriz do triangulo ABC.
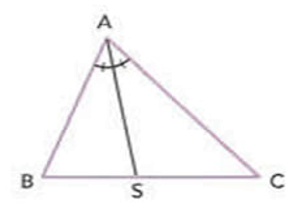
Por definição, teremos: bissetriz de um triângulo é o seguimento que tem uma extremidade em um vértice do triângulo, divide o ângulo ao meio e tem a outra extremidade no lado oposto a esse vértice.
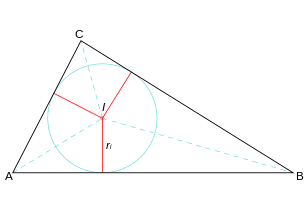
Em todo triângulo, as três bissetrizes cruzam-se em um mesmo ponto, chamado incentro do triângulo.
A distância desse ponto é igual com relação aos lados desse triângulo. Além disso, se desenharmos uma circunferência inscrita nesse triângulo, o seu centro seria exatamente no ponto de incentro.
Outra importante informação é que, em um triângulo isósceles, a altura relativa à base é também mediana e bissetriz.
No triângulo equilátero, toda altura é também mediana e bissetriz.
Bissetriz dos quadrantes do plano cartesiano
No plano cartesiano, sabemos que os eixos X e Y formam entre si ângulos retos, pois são retas perpendiculares.
Para traçar a bissetriz desses quadrantes, devemos imaginar uma reta que corte exatamente esse ângulo de 90° em dois ângulos congruentes, cada um com 45°.
A função f(x) = x é conhecida como função identidade, caso particular da função linear. O gráfico da função identidade f(x) = x é a bissetriz dos 1º e 3º quadrantes.
Por outro lado, a equação da reta bissetriz dos quadrantes pares será f(x) = – x.
Se o ponto P(x, y) pertence à bissetriz dos quadrantes ímpares, as coordenadas de P são iguais, ou seja, x=y. Assim, P tem coordenadas tais que P(a, a), com a ∈ R.
Por outro lado, se o ponto P(x, y) pertence à bissetriz dos quadrantes pares, as coordenadas de P são simétricas, ou seja, x= -y. Assim, P tem coordenadas tais que P(a, -a), com a ∈ R.
Teorema da bissetriz interna
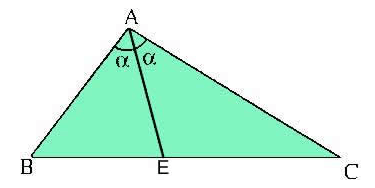
Desenhe o triangulo ABC, sendo o vértice A oposto ao seguimento BC. Trace a bissetriz do ângulo BÂC. O ponto em que a bissetriz encontra o seguimento BC será chamado de E.
Essa bissetriz formou dois ângulos α. Os seguimentos opostos aos ângulos são proporcionais aos seguimentos adjacentes.
Teremos, então:
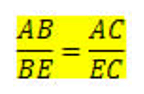
Como mostra a figura abaixo:
Teorema da bissetriz externa
Em um triângulo ABC, faça o prolongamento dos seguimentos BA e BC.
Agora, observe o ângulo externo ao vértice A e trace a sua bissetriz externa. Em um momento, essa bissetriz irá encontrar o prolongamento do seguimento BC.
Com isso, podemos observar na figura que os seguimentos x e y são proporcionais aos lados adjacentes b e c.
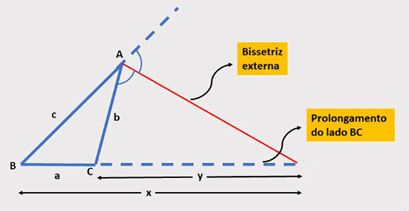
Teremos, então: X/C = V/b.
Exercícios Resolvidos
1) Determine quais são as coordenadas genéricas (em função de a, por exemplo) dos pontos pertencentes à bissetriz dos quadrantes:
a) Ímpares (1º e 3º)
b) Pares (2º e 4º)
Respostas:
a) P(a,a)
b) P(a, -a)
2) Dado o triângulo abaixo, encontre a medida AC.
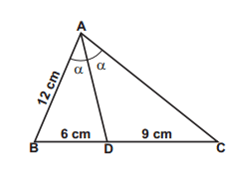
Resposta:
Pelo teorema, faremos:
12/6 = AC/9
6.AC = 108
AC = 108/6
AC = 18 cm
