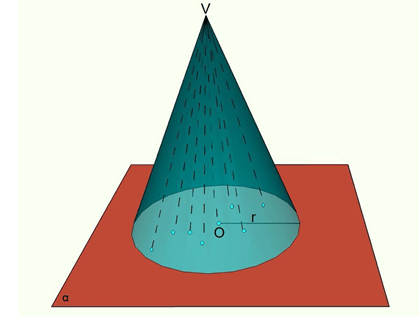
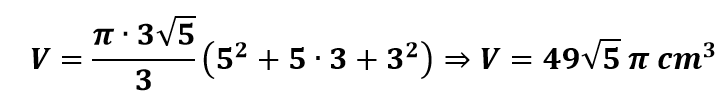O cone é uma forma tridimensional que não tem sua superfície formada apenas por polígonos, nem possui faces ou arestas. Um exemplo são os cones de trânsito, a casquinha de sorvete, etc.
O cone também pode ser definido de maneira mais formal como sendo a figura geométrica formada pela reunião de todos os segmentos de reta que têm uma extremidade no ponto V e a outra num ponto do círculo C.
Num cone, como mostra a figura abaixo, podemos destacar os seguintes elementos:
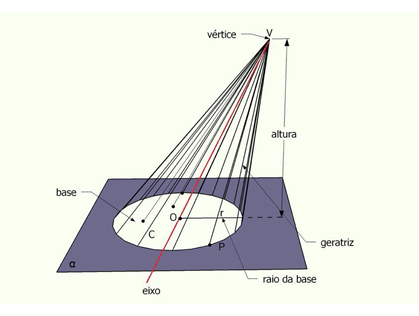
A tabela, a seguir, descreve cada um desses elementos de acordo com a figura.

Um cone pode ser classificado como oblíquo ou reto, conforme a inclinação da reta VO, sendo O centro da base, em relação ao plano da base.
Cone reto
Um cone se diz reto, ou de revolução, quando o eixo, ou a reta VO é perpendicular ao plano da base. Ele pode ser facilmente obtido pela rotação de um triângulo em torno da reta suporte de um dos catetos.
Seção meridiana e cone equilátero
Seção meridiana de um cone reto é a interseção dele com um plano que contém o eixo. No cone circular reto, a seção meridiana é um triângulo isósceles, como mostra a figura.
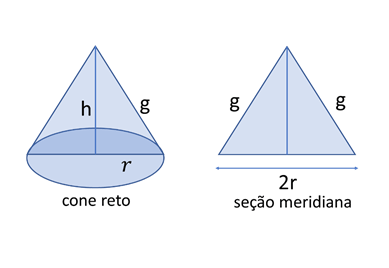
Considerando o triângulo, pode-se estabelecer a seguinte relação num cone circular reto:
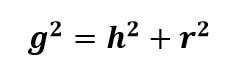
Além disso, quando a secção meridiana de um cone for um triângulo equilátero, ou seja, g = 2r, então, o cone se diz equilátero.
Áreas da superfície de um cone circular reto
Planificando a superfície do cone da figura, temos:
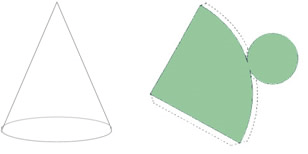
Área da base (Sb)
A base é um círculo de raio r, portanto a área é dada por : Sb = πr2 :
Área lateral (Sl)
A área da superfície lateral corresponde à área de um setor circular de raio g. Nesse caso, para calcular a área da superfície lateral, podemos estabelecer uma regra de três simples ou usar a fórmula geral para a área do setor circular, dada por:
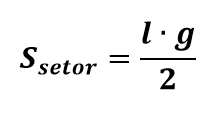
Para a superfície lateral do cone, podemos considerar que l = π2 , portanto:
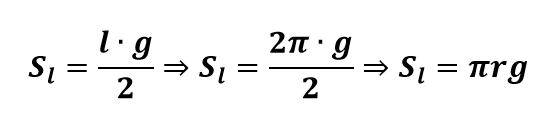
Área total (St)
A superfície total de um cone é a reunião da superfície lateral com o círculo da base. A área dessa superfície é chamada área total. Em linguagem matemática, ela pode ser expressa por:
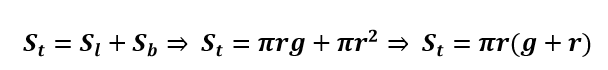
Exemplo
Um cone de revolução tem altura 30m e geratriz 34m. Calcule a área lateral e a total.
Resolução
Primeiramente, é preciso encontrar o valor do raio da base usando a seguinte relação: g2 = h2 + r2. Assim:
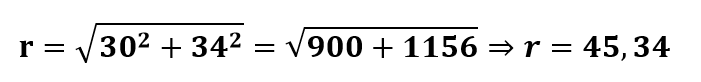
A área lateral é dada por:
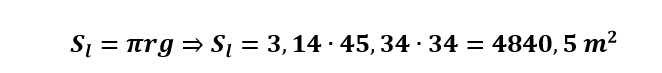
A área total é dada por:
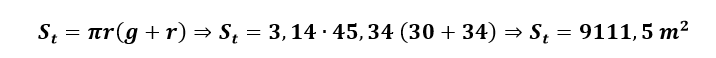
Volume do cone
Usando o Princípio de Cavalieri, temos que o volume V de um cone circular reto, de raio r e altura h, é dada por:
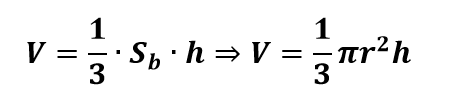
Exemplo
Em um cone circular reto, de altura 12cm, a área total vale 90πcm2 e o volume é 90πcm3 . Calcule o raio da base e a geratriz.
Resolução
Note que podemos determinar a área da base isolando Sb da seguinte equação do volume do cone:
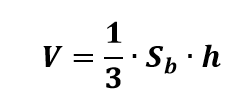
Assim:
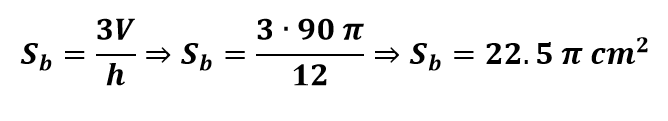
Em seguida, o raio pode ser obtido após a seguinte manipulação algébrica:
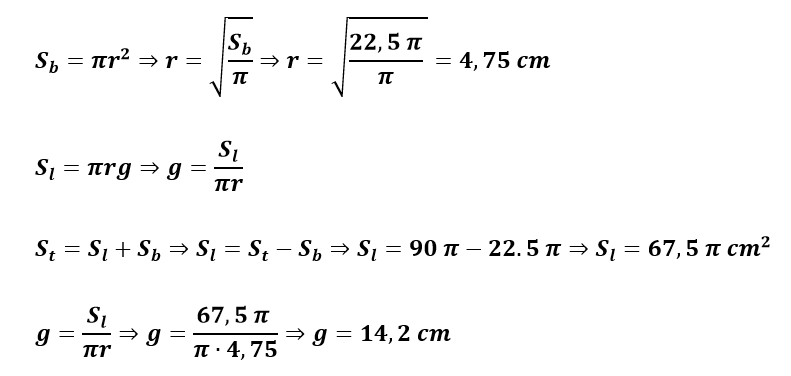
Volume do tronco de cone circular reto
Quando interceptamos um cone por um plano α, que é paralelo à base e não passa pelo vértice, determinamos dois sólidos:
- Outro cone de mesmo vértice;
- Tronco de cone de bases paralelas.
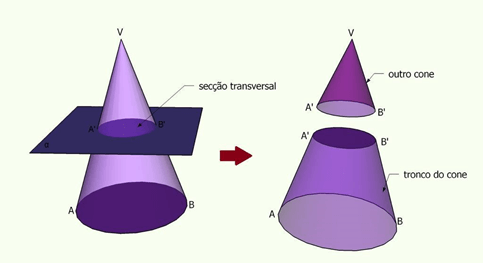
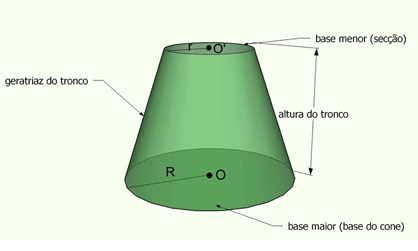
Para determinar o volume do tronco, vamos usar a figura, abaixo:
Nesse caso, a fórmula do volume do troco de um cone é:
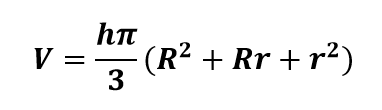
Exemplo:
Vamos calcular o volume de um tronco de cone reto de bases paralelas, cuja altura mede 3√5 cm, e os raios das bases medem 3cm e 5cm.
Resolução
O volume é dado diretamente por: