Medidas de tendência central, como média aritmética, moda e mediana, têm como objetivo concentrar em um único número os diversos valores de uma variável quantitativa. Porém, existem situações em que elas são insuficientes.
Há casos em que os números utilizados para calcular essa medida de tendência central possuem uma diferença muito grande, portanto, é conveniente utilizar medidas que expressem o grau de dispersão de um conjunto de dados. As mais usadas são a variância e o desvio padrão.
Desvio padrão mostra o quanto uma média amostral tem de dispersão, sendo a raiz quadrada da variância. Veja, a seguir, no Gestão Educacional, como calculá-lo.
Medida de dispersão
Vamos imaginar duas situações distintas.
Para passar de bimestre, um aluno deve ter a média das notas de suas duas provas maior ou igual a 5. Se o aluno fez a primeira prova e tirou 8 e na segunda obteve 9, sua média foi 8,5. Só essa informação foi suficiente para saber que o aluno conseguiu passar de bimestre.
Agora, imagine que você precisa organizar uma atividade para um grupo de 6 pessoas e recebe a informação de que a média da idade do grupo é de 20 anos.
Vamos observar alguns grupos possíveis:
- Grupo A: Todos possuem 20 anos.
Média = (20 + 20 + 20 + 20 + 20 + 20) / 6 = 20 anos.
- Grupo B: 22 anos; 23 anos; 18 anos; 19 anos; 20 anos; 18 anos.
Média = 20 anos.
- Grupo C: os integrantes possuem 6 anos; 62 anos; 39 anos; 4 anos; 8 anos; 1 ano.
Média = (6+ 62 + 39 + 4 + 8 + 1) / 6 = 20 anos.
Como você pode perceber, no caso do grupo A, saber que a média tem 20 anos até ajudaria. Porém, no caso do grupo C, existe uma diferença entre as idades muito grande, portanto, não é suficiente saber apenas a média.
Por isso, é difícil montar a atividade apenas com essa informação, pois, nesse caso, mostramos que podem existir grupos com características totalmente diferentes. No grupo A não houve dispersão, pois ele é mais homogêneo que o grupo B.
Vamos entender, agora, como usar o desvio padrão para calcular o grau de dispersão de medidas de tendência central.
Variância
A variância mostra o quão distante cada valor do conjunto está da média central. Ou seja, em um conjunto com n valores, tome os desvios dos valores Xi dos conjuntos em relação à média aritmética (Xi – MA).
A soma desses desvios deve, então, ser igual a zero:
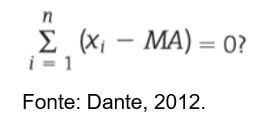
Uma opção possível, então, é considerar o quadrado dos desvios:
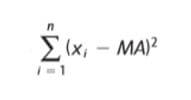
E expressar a variância como a média desse quadrado, ou seja, a fórmula para calcular a variância será:
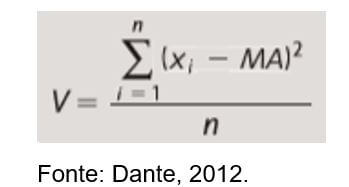
Vamos observar os exemplos acima para tratar disso, calculando sua variância:
- Grupo A: (20; 20; 20; 20; 20; 20)
MA = 20 anos
Desvios: 20-20 = 0
Variância (V) = 0
Quando todos os valores são iguais, dizemos que não houve dispersão, portanto, a variância é igual a zero.
- Grupo B: (22; 23; 18; 19; 20; 18)
MA = 20 anos
Desvios: 22 – 20 = 2; 23 – 20 = 3; 18 – 20 = 2; 19 – 20 = 1; 20 – 20 = 0; 18 – 20 = 2
V = (2² + 3² + (-2)² + (-1)² + 0² + (-2)²) / 6 = 3,6
- Grupo C: (6; 62; 39; 4; 8; 1)
MA = 20
Desvios: 6 – 20 = 14; 62 – 20 = 42; 39 – 20 = 19; 4 – 20 = 16; 8 – 20 = 12; 1 – 20 = 19
V = ((-14)² + 42² + 19² + (-16)² + (-12)² + (-19)²) / 6 = 513,6
Perceba que o grupo A não tem dispersão e que o grupo C tem dispersão maior que o grupo B.
Desvio padrão
Como você pode perceber, não é possível expressar a variância na mesma unidade dos valores da variável, uma vez que os desvios são elevados ao quadrado. Então, definiu-se a medida de dispersão chamada desvio padrão.
O desvio padrão DP é a raiz quadrada da variância. Ele facilita a interpretação dos dados, pois é expresso na mesma unidade.
Continuando a análise daqueles exemplos, teremos:
- Grupo A: DP = √0 = 0 ano;
- Grupo B: DP = √3,6 = 1,9 ano;
- Grupo C: DP = √513 = 22,6 anos.
A variância e o desvio padrão são números positivos ou nulos. Quanto mais próximo de 0 é o desvio padrão, mais homogênea é a distribuição dos valores.
Lembre-se: o desvio padrão é expresso na mesma unidade da variável!
Resumindo, segundo Dante (2012), se X1, X2, X3, …, Xn são os n valores de uma variável quantidade x, temos:
- A média aritmética dos valores de x:
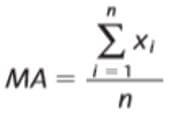
- A variância de x:
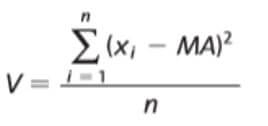
- O desvio padrão de x:
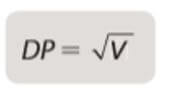
Exercícios Resolvidos
Em um treinamento de salto em altura, os atletas realizaram 4 saltos cada um. Vejamos as marcas obtidas por três atletas:
- Atleta A: 148cm, 170cm, 155cm e 131cm;
- Atleta B: 145cm, 151cm, 150cm e 152cm.
Qual deles foi mais regular?
RESPOSTA:
Calculando a MA de cada atleta:
Atleta A: MA = (148 + 170 + 155 + 131)/4 = 151cm
Atleta B: MA = 149,5cm
Calculando a variância para saber a maior regularidade:
Atleta A: V = (148 – 151)² + (170-151)² + (155-151)² + (131-151)² / 4 = 196,5
DP = √196,5 = 14cm
ATLETA B: V = (-4,5)² + (1,5)² + (0,5)² + (2,5)² / 4 = 7,25
DP = √7,25 = 2,7cm
Logo, o atleta B foi mais regular, pois o DP foi menor.
