A equação exponencial são os tipos de expressões matemáticas incógnitas (o x da questão). Essa fórmula algébrica foi desenvolvida pelo matemático francês René Descartes, no século XVII, representando um grande avanço científico para a época.
Para resolver equações exponenciais, é preciso, primeiramente, saber como solucionar equações do primeiro grau e entender como funcionam as potências.
O que são equações exponenciais
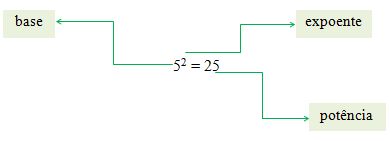
Antes de resolver qualquer equação de potenciação, lembre-se de saber denominar corretamente cada representação matemática, conforme indica a imagem:
- A base é o número que está embaixo;
- O expoente é o número que está elevado;
- O número de resultado é a potência.
No caso da equação exponencial, a incógnita deverá estar no expoente (número elevado). Desse modo, um exemplo de equação exponencial é:
4 x = 12 ou 3 y + 6 = 27
Como resolver uma equação exponencial – Passo a Passo
Exemplo de equação: 3 x = 27
1 – Observe a equação exponencial e lembre-se da regra número 1: a x = a y, ou seja, x =y. Em outras palavras, se as potências da mesma base são iguais, expoentes também serão;
2 – O número que deverá ir no expoente é aquele que multiplicado a quantidade de vezes do seu valor pela base resultará na potência (resultado). Portanto, nesse caso, o expoente seria 3, porque:
3 x = 33
3 x = 3 x 3 X 3
3 – Aqui, as bases são iguais, dessa forma, basta cortá-las para termos o resultado:
x = 3
Equação exponencial com bases diferentes – Como igualar?
Mas, e se as bases não forem iguais? Calma! Vamos repetir o passo a passo com outro exemplo:
Equação: 17 4x+1 = 1
1 – Sempre que tiver o número 1 de algum lado, que número elevar para chegar a número 1? Será o mesmo esquema que qualquer número elevado a 0. Por isso, a equação fica:
17 4x+1 = 170
2 – Conseguimos, agora, igualar as bases – mais uma vez bastará cortá-las:
4x + 1 = 0
4 x = – 1
x = -1/4
Se ainda não entendeu como igualar bases, confira mais exemplos no vídeo, abaixo:
Equação exponencial com fração
Quando há frações no denominador, é preciso pensar que potência pode ser substituída por aquela fração, como no exemplo, abaixo:
Exemplo de equação:
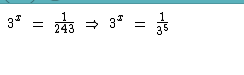
Sabe-se que a fração é a mesma coisa que 3-5. Portanto, podemos reescreve-la utilizando isso:
3x = 3 -5
Mais uma vez conseguimos igualar as bases, ou seja, é hora de cortá-las para encontrar o valor do x:
x = – 5
Equação exponencial com raiz quadrada
O princípio de solução de uma equação com raiz quadrada é o mesmo do que os demais, portanto, é necessário igualar as bases. Veja o exemplo:
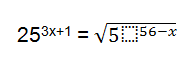
Agora, precisamos fatorar a equação, ou seja, igualar as bases substituindo-as por novos números em potência, como:
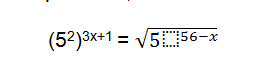
Para igualar a raiz quadrada, é preciso aplicar as propriedades de radiação com a potenciação. Já aproveitamos, também, para multiplicar a base:
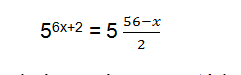
Agora que as bases estão igualadas, é possível cortá-las. Então, a equação fica:
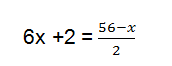
Deve-se passar o 2 para o outro lado e a fração (divisão) torna-se sinal negativo, o que dá: -2 -2, ou seja, -4:
12 x +x = 56 – 2 – 2
12 x + x = 56- 4
Vê-se que x+x é o mesmo que acrescentar uma unidade à base. Por isso, a equação fica:
13 x = 52
Por fim, basta terminar de resolver a equação para chegar ao resultado:
x = 52/13
x = 4
Agora que você já aprendeu como resolver as equações exponenciais, treine bastante e converse com o seu professor para tirar eventuais dúvidas!

