Equações irracionais são aquelas em que pelo menos uma das incógnitas está presente dentro de um radical. Lembrando que a incógnita pode ser qualquer letra ou símbolo, mas costumamos usar a letra x. Isso ficará mais claro nos exemplos abaixo:
Exemplos de equações irracionais
Confira abaixo alguns exemplos de Equações Irracionais:
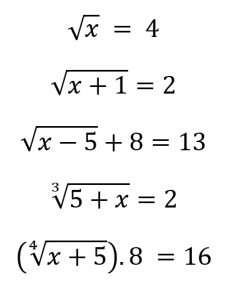
Como resolver?
O objetivo principal é “tirar” o x e o que o acompanha, o radicando, de dentro do radical. Para isso, deve-se eliminar a radiciação, elevando os dois lados da equação pelo mesmo número do índice do radical
. É claro que isso deve ser feito apenas depois que haja apenas o radical de um dos lados da equação. Isso ficará mais claro no exemplo 3. Além disso, se chegarmos em uma equação do segundo grau onde há duas incógnitas, é preciso checar qual delas é a correta substituindo na equação inicial.
Vejamos abaixo a resolução dos exemplos vistos acima:
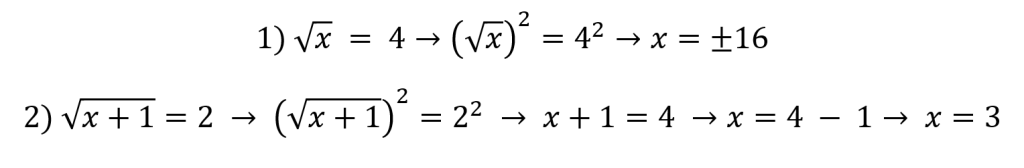
No terceiro exemplo, teríamos problema se já elevássemos os dois lados por dois, pois teríamos o termo:
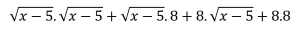
Que é o que aprendemos como “quadrado do primeiro mais duas vezes o primeiro vezes o segundo mais o quadrado do segundo”. Então por isso precisamos deixar o radical sozinho antes de mais nada!
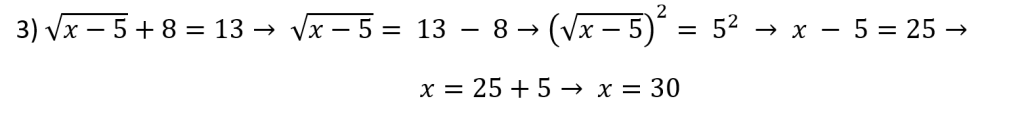
Agora no exemplo 4, o índice é três, então precisamos elevar ao cubo
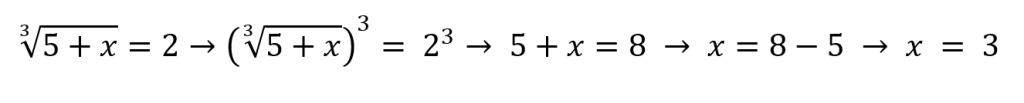
Seguindo a mesma lógica para o quinto exemplo:
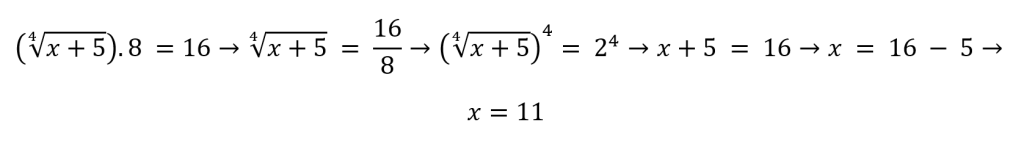
Então primeiro deixe só o radical contendo a incógnita e então eleve dos dois lados com o mesmo número do índice. Depois, é só isolar a incógnita e encontrar o valor!
Referência
Fonte: LANG, Serge. Basic mathematics. Frank Brothers, 1988.

