Fatoração – O que é? Tipos, Exemplos, Fórmulas e Exercícios Resolvidos
Fatorar significa decompor em fatores, ou seja, escrevemos um número ou uma expressão como produto de fatores.
Esse recurso é empregado em cálculos algébricos, principalmente para simplificar expressões. Existem vários casos de fatoração, nos quais utilizamos cada um analisando as características do polinômio a ser fatorado.
Conheça, a seguir, os métodos algébricos para realizar a fatoração e veja exemplos de cada um desses casos.
Primeiro caso: fator comum em evidência
Caso você observe que em um determinado polinômio existe um fator comum, ou seja, um número ou uma incógnita que se repete, pode-se colocar esse fator comum em evidência.
Observe o exemplo abaixo:
- 2x² + 2xy
Nesse caso, temos que cada uma das parcelas possui o fator comum 2x. Vamos então colocá-lo em evidência:
- 2x (2x + y)
Outro exemplo: vamos fatorar a expressão 6x²y + 9x² + 12x. Observe que 3 é fator comum dos coeficientes 6, 9 e 12 e que x também é um fator comum de todas as parcelas.
Fatorando, teremos: 3x(2xy + 3x + 4).
Para verificar se a fatoração está correta, basta desenvolver o produto e observar se volta ao polinômio inicial.
Segundo caso: agrupamento
Observe o seguinte polinômio:
- ax + 2a + 5x + 10
Não existe fator comum nos quatro termos. Mas, podemos agrupá-los de forma convincente. Observe:
- a(x + 2) + 5(x + 2)
Veja que, agora, (x + 2) é fator comum – (a + 5).(x + 2). Ou seja, agrupamos alguns termos para que eles formassem fatores em comum.
Terceiro caso: trinômio quadrado perfeito
O quadrado da soma e o quadrado de uma diferença nos dão trinômios como resultado.
- (x+5)² = x² + 10x + 25
- (a-7)² = a² – 14a + 49
Do mesmo modo que podemos “abrir” esse quadrado perfeito, podemos fazer o caminho inverso.
- X² + 10x + 25
X² foi obtido fazendo o quadrado de x. 10x foi obtido pelo dobro do produto de x e 5. 25 foi obtido fazendo 5 ao quadrado.
Para descobrirmos isso, utilizamos as igualdades a seguir:
- (a+b²) = a² + 2.ab + b²
- (a-b)² = a² – 2ab + b²
Com isso, podemos fatorar qualquer trinômio apenas pensando da forma inversa.
Quarto caso: diferença de dois quadrados
Para realizar fatorações dessa maneira, vamos lembrar disso:
- x² – y² = (x + y) (x – y)
Dessa maneira, quando olhamos para expressões nas quais dois termos podem ser escritos como a diferença de dois quadrados, iremos utilizar esse caso de fatoração.
Observe a seguinte expressão:
- 16x² – 25
O fator 25 pode ser escrito como 5². 16x² também pode ser escrito como (4x)². Para descobrirmos isso, basta buscar a raiz quadrada de cada um desses termos, como é feito abaixo: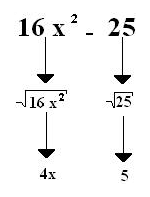
Quinto caso: soma de dois cubos
Para fazermos fatorações dessa maneira, precisamos lembrar da soma de dois cubos:
- a³ + b³ = (a + b). (a² – ab + b²)
Se em uma expressão você observar que dois fatores podem ter raiz cubica, esse caso de fatoração pode se encaixar perfeitamente.
Observe o exemplo:
- 125x³ + 8.
Podemos extrair a raiz cubica de 125x³ e de 8. A raiz cúbica de 125x³ é 5x e a de 8 é 2. Portanto, podemos escrever essa expressão da seguinte maneira: 125x³ + 8 = (5x + 2)(25x² -10x + 4).
Sexto caso: diferença de cubos
O raciocínio é o mesmo do caso anterior. Porém, devemos lembrar da fórmula da diferença de dois cubos:
- X³ – y³ = (x – y) (x² + xy + y²)
Veja um exemplo:
- 27x³ -125 = (3x –5)(9x² + 15x + 25)
Resumo do conteúdo
- Quadrado da soma: (a + b)2 = a2 + 2.a.b + b2
- Quadrado da diferença: (a – b)2 = a2 – 2.a.b + b2
- Produto da soma pela diferença: a2 – b2 = (a + b) . (a – b)
- Cubo da soma: (a + b)3 = a3 + 3.a2.b + 3.a.b2 +b3
- Cubo da diferença: (a – b)3 = a3 – 3.a2.b + 3.a.b2 – b3
- Soma entre dois cubos: a3 – b3 = (a + b) . (a2 – a.b + b2)
- Diferença entre dois cubos: a3 – b3 = (a – b) . (a2 + a.b + b2)
Exercícios resolvidos
1) Fatore os polinômios abaixo colocando algum fator em evidência:
A) x(x – 4) + 6(x – 4)
B) 3a(4a + 2) + 5(4a + 2)
C) (x +1)(x – 3) + 2(x+1)
RESPOSTA
A) Perceba que o termo (x – 4) está se repetindo nos dois termos. Vamos colocá-lo em evidência.
(x – 4)(x+6)
B) O termo (4a + 2) está se repetindo. Vamos colocá-lo em evidência (4a + 2)(3a + 5)
C) O termo (x + 1) está se repetindo, vamos então colocá-lo em evidência.
(x+1)[(x+3) + 2) = (x + 1)(x + 5)
2) Fatore as seguintes expressões usando agrupamento:
A) ab + 3b –7a –21
B) x² + xy + x + y
RESPOSTA
A) b(a+3) -7(a+3)
Surge um fator comum: (a+3).
(a+3) (b-7)
B) Colocando x em evidência e 1 também:
x(x+y) + 1(x+y)
Temos um fator comum agora: (x+y).
(x+1).(x+1).
3) Fatore as expressões a seguir:
A) 9x² + 60x + 100
B) x² -1
RESPOSTA
A) 9x² + 60x + 100 é um trinômio quadrado perfeito. Vamos utilizar aqui o segundo caso de fatoração.
9x² + 60x + 100 = (3X + 10)²
B) x² – 1 é a diferença entre dois quadrados, pois 1 pode ser escrito como 1².
X² -1 = (x + 1) (x – 1)






Deixe seu comentário