A fatorial de um número n! será o produto dos números inteiros consecutivos menores e igual a n. Indicamos por n! e lemos “fatorial de n” ou “n fatorial”.
Desde a antiguidade, usamos esse método para alterar a posição de elementos, com a finalidade de criptografar uma mensagem. A seguir, veja a definição e como usar o fatorial de um número.
O que é fatorial de um número?
Definimos fatorial de um número como: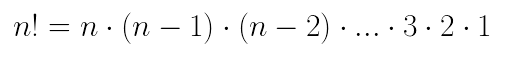
Exemplos
- Fatorial de 0: 0! = 1;
- Fatorial de 1: 1! = 1;
- Fatorial de 2: 2! = 2 . 1 = 2;
- Fatorial de 3: 3! = 3 . 2 . 1 = 6;
- Fatorial de 4: 4! = 4 . 3 . 2 . 1 = 24;
- Fatorial de 5: 5! = 5 . 4 . 3 . 2 . 1 = 120;
- Fatorial de 6: 6! = 6 . 5 . 4 . 3 . 2 . 1 = 720;
- Fatorial de 7: 7! = 7 . 6 . 5 . 4 . 3 . 2 . 1 = 5.040;
- Fatorial de 8: 8! = 8 . 7 . 6 . 5 . 4 . 3 . 2 . 1 = 40.320;
- Fatorial de 9: 9! = 9 . 8 . 7 . 6 . 5 . 4 . 3 . 2 . 1 = 362.880;
- Fatorial de 10: 10! = 10 . 9 . 8 . 7 . 6 . 5 . 4. 3 . 2 . 1 = 3.628.800.
Além disso, podemos escrever: n! = N . (n – 1). Isto é, por exemplo: 15! = 15 . 14!
Fórmulas da análise combinatória que usam fatorial
Em análise combinatória, usamos o fatorial para resolver exercícios de permutação, arranjo e também combinação.
- Permutação simples:
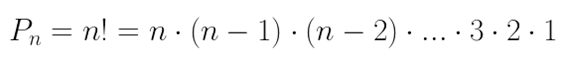
- Arranjo Simples:
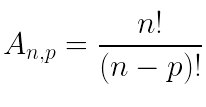
- Combinação:
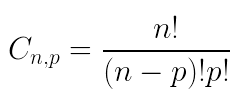
Operações com fatoriais
Para realizar as operações com fatoriais, devemos primeiro resolver o produto. Veja, a seguir, alguns exemplos:
- Soma: 5! + 3! = (5 . 4 . 3 . 2 . 1) + (3 . 2 . 1) = 120 + 6 = 126;
- Subtração: 5! – 4! = (5 . 4 . 3 . 2 . 1) – (4 . 3 . 2 . 1) = 120 – 24 = 96.
Nesse momento, poderíamos até pensar erroneamente que 5! – 4! = 1! = 1. Vimos acima que isso não é verdade.
- Multiplicação: 2! . 4! = (2 . 1) . (4 . 3 . 2 . 1) = 2 . 24 = 48.
- Divisão: no processo de divisão, podemos simplificar, como faremos abaixo:
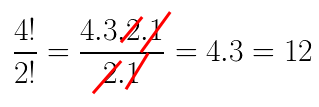
Simplificações
O único momento em que é possível simplificar fatoriais, como vimos acima, é no processo de divisão. Portanto, podemos dizer que: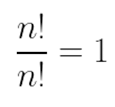
Iremos utilizar isso também no exemplo abaixo:
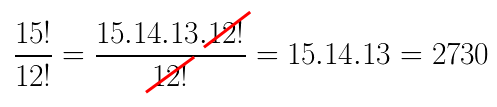Isso pode ser usado em todos os exercícios que envolvam divisão de dois fatoriais iguais.
Exercícios resolvidos
1) Se (n + 4)! + (n + 3)! = 15(n + 2)! Então:
- a) n = 4
- b) n = 3
- c) = n = 2
- d) n = 1
- e) n = 0
Resolução:
(n + 4)! + (n + 3)! = 15(n + 2)!
(n + 4) (n + 3) (n + 2)! = 15(n + 2)!
(n + 4) (n + 3) = 15
n² + 8n + 15 = 15
n² + 8n = 0
Encontrando as raízes dessa equação do segundo grau, temos que:
n = 0 ou n = -8. Nesse caso, a alternativa que convém é a alternativa e.
2) Quantos são os números de quatro algarismos que podemos escrever com os algarismos 2, 4, 6 e 8? E de quatro algarismos distintos?
Resolução:
Quando os algarismos podem se repetir, podemos ter números como 2222, 6688, e assim por diante.
Portanto, podemos formar: 4 . 4 . 4 . 4 = 256 números.
Porém, para calcular números de quatro algarismos distintos, vamos utilizar o fatorial: 4! = 4 . 3 . 2 . 1 = 24 números.
Portanto, formamos 256 números com os algarismos 2, 4, 6 e 8. Entretanto, sem repetir, podemos formar 24 números com esses mesmos algarismos.
3) Quantos são os anagramas da palavra amor?
Resolução:
Fazendo a permutação das quatro letras dessa palavra, ou seja, trocando-as de lugar, teremos: 4! = 4 . 3 . 2 . 1 = 24 anagramas.
