Compreende-se que a Matemática é dividida em duas partes: a geometria e a álgebra, que se complementam e são igualmente importantes. A matemática é conhecida por ser icônica, ou seja, faz uso de representações, como desenhos, gráficos ou símbolos, para auxiliar na produção de um raciocínio. A geometria, por sua vez, utiliza ilustrações que simbolizam figuras geométricas.
A geometria euclidiana estuda as formas que estão à nossa volta, sendo assim, muito intuitiva. Ela tem esse nome porque, graças à Euclides de Alexandria – matemático grego, nascido no século III a.C. – os conhecimentos dessa área se desenvolveram. Euclides arrumou tudo o que sabia sobre geometria na época em 13 livros da coleção “Os Elementos”.
A seguir, veremos partes importantes sobre a geometria euclidiana: figuras bidimensionais e suas características.
Figuras bidimensionais: o que são?
As figuras geométricas podem ser representadas em uma, duas, três ou n dimensões. Quando se tratam de figuras de duas dimensões, as chamamos de bidimensionais, isto quer dizer que é possível observar tanto largura quanto comprimento da figura.
Como exemplo disso, temos o quadrado. Porém, a profundidade do quadrado é inexistente, porque ele não tem três dimensões.
O espaço bidimensional é denominado “plano”. Desse modo, toda a geometria plana trata de figuras bidimensionais.
Polígonos
Quando se trate de figuras planas, utiliza-se o termo “polígono” (poli = muitos; gono = ângulo), que nada mais é que um contorno, um segmento de reta que não se cruza em um único plano.
Os polígonos se distinguem por serem convexos ou não convexos. Polígonos convexos são aqueles em que há um segmento que une dois pontos do seu interior, estando inteiramente contido nessa região.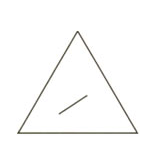
No caso dos polígonos não convexos, o segmento de reta que une dois pontos não está inteiramente contido na região limitada por esse polígono.
Um polígono convexo possui diversos elementos, são eles: vértices, que são os pontos, por exemplo: A, B, C, D, E; lados, que se tratam dos seguimentos de reta AB, BC, DE, EF e FA; diagonais, que são os segmentos de reta que ligam um vértice a outros vértices que não vêm em seguida: AC, AD, AE, BD, BE, BF, CE, CF, DF (linhas tracejadas na imagem abaixo).
Outro elemento de um polígono convexo é o ângulo interno (ângulos laranjas), que são ângulos formados por dois lados consecutivos. Por fim, não podemos nos esquecer dos ângulos externos (ângulos lilás), que são ângulos formados por um lado e pelo prolongamento do lado consecutivo a este.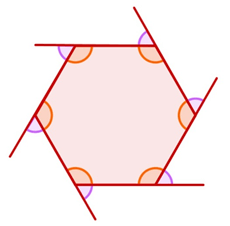
Vale ressaltar que em todo polígono convexo, o número dos seus elementos (vértices, lados, ângulos internos e externo) são os mesmos.
Classificação dos polígonos
Podemos classificar um polígono de acordo com o número de lados que ele possui. Os mais conhecidos são: o triângulo (tri = três): três lados; quadrilátero (quadri = quatro): quatro lados; pentágono (penta = cinco): cinco lados; hexágono (hexa = seis): seis lados; heptágono (hepta = sete): sete lados; octógono (octo = oito): oito lados; eneágono (ênea = nove): nove lados; decágono (deca = dez): dez lados.
Polígonos regulares
Um polígono convexo é denominado “polígono regular” quando possui todos os lados com a mesma medida e também todos os ângulos internos de mesma magnitude.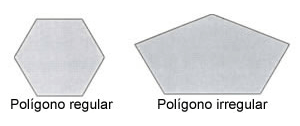
O triângulo é um polígono convexo muito importante, porque, por meio dele, pode-se formar todas as outras figuras poligonais.
A forma mais usual de classificar triângulos, os segmenta em três tipos: equiláteros, no qual todos os lados têm a mesma medida; isósceles, que possui dois lados de mesma medida; e escaleno, caso em que todos os lados são diferentes.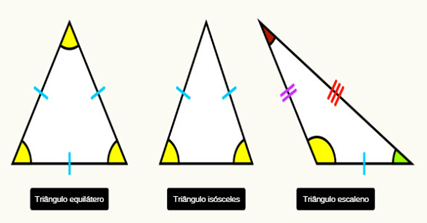
Quadriláteros
Os quadriláteros são classificados de acordo com o paralelismo de seus lados, o tamanho de seus ângulos e de seus lados. Temos, assim, por exemplo, o trapézio, que é um quadrilátero que tem, no mínimo, um par de lados paralelos.
Os lados que são paralelos são denominados “bases do trapézio”. Existem trapézios escalenos, isósceles e retângulos.
Outro tipo de quadrilátero são os paralelogramos, no qual os lados são dois a dois paralelos. Desse modo, consideramos o paralelogramo como um tipo de trapézio.
Em um paralelogramo, os lados e os ângulos opostos possuem o mesmo tamanho e os ângulos consecutivos juntos resultam em 180º. No paralelogramo as diagonais se cortam na metade da figura.
Existe, também, o quadrilátero tipo retângulo, que nada mais é que um paralelogramo com ângulos retos. As suas diagonais se cortam no meio e têm o mesmo tamanho.
Não podemos deixar de mencionar o losango, que é um paralelogramo que possui todos os lados do mesmo tamanho. Nesse caso, as diagonais são perpendiculares e se cortam ao meio. O quadrado é um losango.
