Uma das fórmulas mais lembradas por quem já saiu do Ensino Médio é a fórmula de Bhaskara, utilizada na resolução das equações de segundo grau. Essas também são chamadas de equações quadráticas, isso porque determinam os valores de uma equação polinomial de segundo grau.
O nome vem de um grande matemático que criou a fórmula, Bhaskara Akaria, indiano dedicado à matemática, astronomia e astrologia. Veja, a seguir, mais sobre essa fórmula.
Fórmula de Bhaskara: Como Funciona?
A fórmula é composta pelos seguintes elementos:
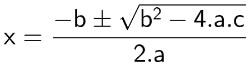
Cada um desses símbolos representa uma parte da equação. São eles:
- x: variável, conhecida como incógnita;
- a: coeficiente quadrático;
- b: coeficiente linear;
- c: coeficiente constante.
A equação
O discriminante da equação é expressada pela letra grega Delta (Δ), que faz parte da fórmula, que é a raiz expressa da fórmula. DICA: é necessário resolver essa raiz quadrada, antes de inserir os outros valores da fórmula.
Tipos de Equações de Segundo Grau
A fórmula de Bhaskara é usada nas equações de segundo grau, conhecidas como completas; já as incompletas não precisam dela para a resolução.
Completas
Só é possível encontrar os resultados por meio da fórmula de Bhaskara, em que os coeficientes a, b e c são diferentes do valor zero.
Incompletas
Os resultados são encontrados sem usar a fórmula de Bhaskara, em que o coeficiente a é o único que será diferente de zero – enquanto isso, b e c são iguais a zero.
Como usar a fórmula de Bhaskara?
Você apenas precisa substituir os valores respectivos na fórmula de Bhaskara, depois resolver as operações necessárias, então, obter as raízes da equação.
Entenda melhor pelo passo a passo, abaixo:
Como calcular discriminante
A expressão que existe dentro da raiz, na fórmula de Bhaskara, costuma ser representada por Delta. Tem esse nome porque as letras a, b e c são conhecidas como as constantes da equação, em que o valor de Delta pode acontecer de três formas:
- Quando o valor de Delta é maior que zero, essa equação terá duas raízes reais e diferentes;
- Quando o valor de Delta é igual a zero, haverá somente uma raiz;
- Quando o valor de Delta é menor que zero, não há raízes reais.
Substituição da discriminante e dos coeficientes
Agora, basta substituir os valores de Delta e dos coeficientes na equação de segundo grau.
Calcular raízes da equação
Na fórmula de Bhaskara, há dois valores “±”, para os quais deverão ser feitas as duas contas. Nesse caso, para que o número seja positivo ou negativo – geralmente, eles são nomeados como x1 e x2.
