Fórmula de Moivre – Plano de Argand-Gauss, Módulo de número complexo

As fórmulas de Moivre são utilizadas para obtermos a potenciação de um número complexo (zⁿ) ou a raiz enésima de z.

Primeiramente, precisamos entender o que é o plano de Argand-Gauss, como encontrar o módulo de um número complexo, como deixá-lo na forma trigonométrica e, por fim, quais são as fórmulas de Moivre.

Plano de Argand-Gauss

Sabemos que um número complexo z = a + bi pode ser representado de várias formas. Geralmente, vemos sempre sua forma algébrica, dada por z = a + bi. Porém, podemos representar esse número complexo z por um par ordenado de números reais e assim representá-los geometricamente no plano cartesiano.

Assim, se z = a + bi é um número imaginário, podemos escrever que z = (a,b).  Esse par ordenado pode ser associado a um ponto P no plano cartesiano. Portanto, o ponto P tem coordenadas P (a, b).

O plano cartesiano no qual estão representados os números complexos é chamado de plano complexo ou plano Argand-Gauss.

Dizemos que o ponto P (a, b) é a imagem do número complexo a + bi.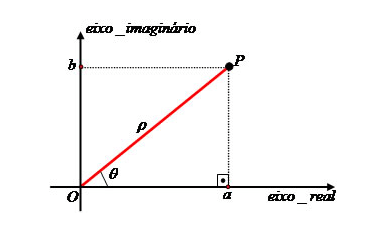Esse plano possui um eixo real (Re) e um eixo imaginário (Im). Para cada número complexo existe um único ponto no plano.

Existe alguns casos específicos, como:

• Números complexos puros: esses números imaginários são do tipo z = 0 + bi e pertencem ao eixo imaginário, pois sua parte real é igual a zero;
• Números complexos reais puros: esses números são do tipo z = a + 0i e pertencem ao eixo real, pois sua parte imaginária é igual a zero;
• Demais números complexos (a + bi), com a ≠ 0 e b ≠ 0: pertencem a vários quadrantes, de acordo com os sinais de a e b.

Módulo de um número complexo

Geometricamente, o módulo de um número complexo é a distância da origem do sistema de coordenadas O à imagem de z.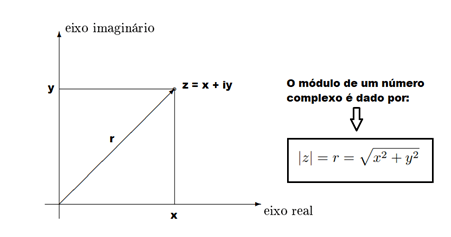Aplicando o Teorema de Pitágoras, temos: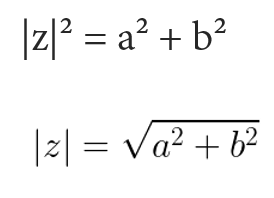

Forma trigonométrica do número complexo

Sabemos que um número complexo z = a + bi é representado por um ponto no plano, de coordenadas (a, b). Essas são as coordenadas cartesianas do ponto z. Veremos, agora, que esse ponto pode ser representado por suas coordenadas polares, que são:

1ª) o módulo do número complexo |z|, que representa a distância do ponto P à origem do plano;

2ª) O angulo θ, em que 0 ≤ θ < 2π, que o vetor Oz forma com o eixo x. Esse ângulo θ é chamado argumento de z (ou argumento principal de z) e indicado por arg(z).

Dizemos que:

• a = |z| . cos θ
• b = |z| . Sem θ

Substituindo esses valores em z = a + bi, temos:

• z = a + bi
• z = |z| . Cos θ + |z| sen θ i
• z = |z|. (cos θ + i . sen θ)

Essa é a forma trigonométrica ou forma polar de z.

Primeira formula de Moivre

Quando elevamos um número complexo a uma potência, utilizamos a primeira fórmula de Moivre.

A potência zⁿ é dada por z = z . z . z . … . z, ou seja, multiplicamos o número z n vezes. Assim, para um número complexo escrito na forma trigonométrica, a primeira formula de Moivre será: Zⁿ = |z|ⁿ [ cos (nθ) + i . sen(nθ) ]

Para n = 0, temos que z⁰ = 1. Para entender melhor como utilizá-la, assista ao seguinte vídeo:

Segunda fórmula de Moivre

Dado um número complexo z e um número natural n, n>1, definimos: a raiz enésima de um número complexo ω tal que ωⁿ  = z.

Encontrar as raízes enésimas de z significa determinar todos os números complexos que são distintos do tipo:  ω = |ω| (cos α + i sen α).

Portanto, definimos a segunda fórmula de Moivre como: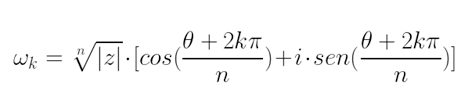É possível obter n-1 raízes distintas desconhecidas de um número complexo. Para isso, usamos: K = 0, 1, 2, … , (n-1).

 

Após k = n-1, os valores começam a se repetir.

Para entender melhor, assista ao seguinte vídeo: