Função afim – O que é? Como calcular? Crescente e Decrescente, Exemplos

Função afim ou função do primeiro grau é toda função polinomial de grau um, em que sua lei de formação é dada por f(x) = ax + b para todo x pertencente aos números reais, desde que existam dois números reais a e b. Essa função associa duas variáveis e pode ser representada por uma reta, ao traçarmos o seu gráfico, sendo a inclinação dessa determinada pelo seu coeficiente angular.

A noção de que quanto mais se aumenta uma grandeza mais se aumenta outra está presente em nosso cotidiano. Nas compras, quanto mais se compra, mais se paga; no preparo de uma receita, quando dobramos as medidas dos ingredientes na receita, mais comida teremos. Tudo isso pode ser relacionado por uma função, pois esta vai associar justamente duas variáveis diretamente proporcionais.

Função afim: casos particulares

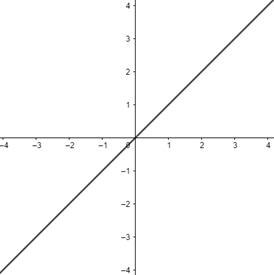
• Função identidade: a função identidade é definida por f(x) = x. Nesse caso, os coeficientes são a = 1 e b = 0.

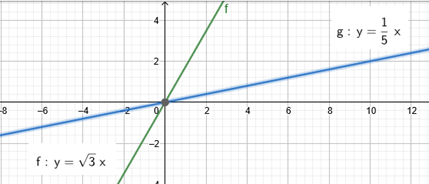
• Função linear: definida por f(x) = ax. Nesse caso, b = 0.

Alguns exemplos são:

• f(x) = -2x
• g(x) = √3 x

• Função constante: definida por f(x) = b. Nesse caso, a = 0.

Alguns exemplos são:

• f(x) = 3
• g(x) = 3/4

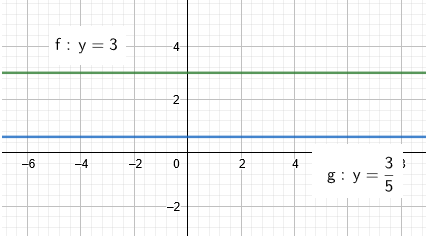
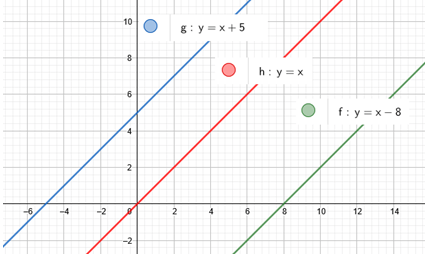
• Translação da função identidade

A função identidade é dada por f(x)= x e é representada pela reta vermelha abaixo. Porém, podemos “movimentá-la” para a esquerda ou direita, por uma translação. Para isso, basta escolher um número b qualquer real e definir a = 1, como mostra os dois exemplos abaixo:

• f(x) = x – 8
• g(x) = x + 5

Coeficientes

Definimos uma função afim como uma função que genericamente é escrita como f(x) = ax + b. Chamamos de coeficiente angular a o número que é multiplicado pela variável x. Esse número determina se a função será crescente ou decrescente.

Já o coeficiente angular b é o ponto onde o gráfico corta o eixo das ordenadas, ou seja, o ponto de coordenadas (0, b). Para confirmar isso, basta atribuir x = 0:

• f(0) = a.0 + b
• f(0) = b

Taxa de variação da função afim

A taxa de variação de uma função é também conhecida como coeficiente angular da função, pois são obtidos da mesma maneira: basta ter dois pontos pertencentes à reta que formaremos o gráfico dessa função.

Sejam dois pontos A (x₁, y₁) e B(x₂, y₂) pertencentes à reta, podemos encontrar a taxa de variação por: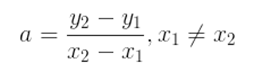A taxa de variação a é sempre constante para cada função afim. Além de mostrar qual é a inclinação da reta, ela indica com qual velocidade o valor da função cresce ou decresce.

Outra maneira de obtê-la é fazer f(1) – f(0).

Função crescente e decrescente

Dizemos que uma função é crescente quando ela apresenta maiores valores para y=f(x), quando também aumentamos os valores de x.

Veja, abaixo, um exemplo de função crescente: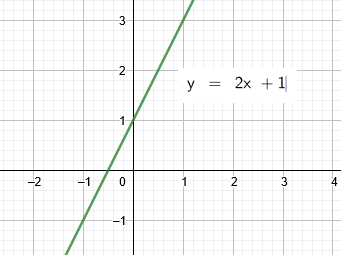Enquanto isso, classificamos uma função como decrescente quando, para maiores valores de x, obtemos menores valores para y=f(x).

Abaixo, veja um exemplo de função decrescente: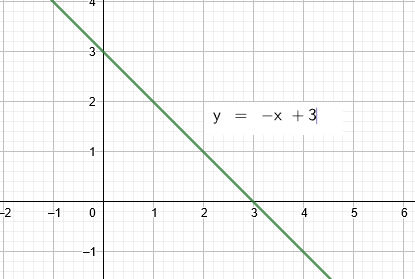O que determina se uma função é crescente ou decrescente é o seu coeficiente angular. Dada lei de formação f(x) = ax + b, se:

• a > 0 : função crescente;
• a < 0 : função decrescente.

Além disso, uma função pode ter intervalos em que ela é crescente e intervalos em que ela é decrescente. Observe o gráfico abaixo da função f(x) = |x|: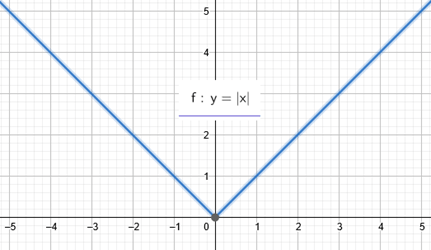Nessa função, para x > 0, temos valores que indicam se tratar de uma função crescente. Para x < 0, temos valores que mostram que a função é decrescente.

Como determinar a função com dois pontos?

Quando conhecemos dois pontos pertencentes a essa função, podemos determinar sua lei de formação.

Dado dois pontos A(x₁, y₁) e B(x₂, y₂), podemos determinar a função que possui esses dois pontos da seguinte maneira:

PASSO 1) Encontrando o coeficiente angular:

Para isso, basta fazer: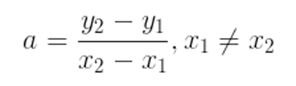PASSO 2) Fazendo a substituição na equação fundamental da reta:

A equação fundamental da reta é dada por: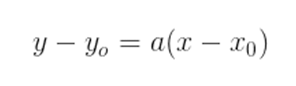As coordenadas (x₀, y₀) podem ser as coordenadas de um ponto qualquer pertencente à reta dessa função. Esse ponto pode, inclusive, ser o próprio ponto A ou B, usados anteriormente.