A função exponencial é definida por f(x) = ax , sendo a a base da função e a variável x o expoente dessa base. Algumas restrições são necessárias para definirmos essa função, como a > 0 e a ≠ 1. Além disso, ela não assume valores menores ou iguais a zero para x.
Conta a lenda que um rei solicitou a seus súditos que inventassem um novo jogo para diminuir o tédio que ele sentia. Um inventor então criou o xadrez e pediu, como recompensa, que colocassem um grão na primeira casa do tabuleiro e o dobro de grãos na casa seguinte, e assim sucessivamente. Para a última casa seriam necessários 263 grãos! Essa famosa lenda persa descreve o modelo exponencial.
Restrições da função exponencial
A função exponencial é uma função de R em R*+, ou seja, seu domínio é definido para todo x real e sua imagem é definida apenas em números reais positivos e não nulos, ou seja, y > 0.
Para que isso ocorra, existem algumas restrições as quais essa função deve obedecer:
- Se a = 1, temos que 1 elevado a qualquer número é igual a 1, então a função seria constante;
- Se a < 0, a função não é definida para alguns expoentes. Por exemplo: se a < 0 e x = 1/2, não haveria ax, pois a função não é definida nos números reais;
- Se a = 0, a função não seria definida para certos expoentes. Por exemplo: caso x seja negativo, não existiria ax, pois a função não é definida só nos números reais.
Gráfico da função exponencial
O gráfico dessa função é chamado curva exponencial e passa sempre pelo ponto (0,1), já que para x = 0, todo número elevado a 0 é igual a 1. Seu D(f) = R e sua Im(f) = R*+. Desse modo, o gráfico não toca o eixo x e não tem pontos nos quadrantes III e IV.
Para a > 1, a função é crescente. Já para 0 < a < 1, a função é decrescente.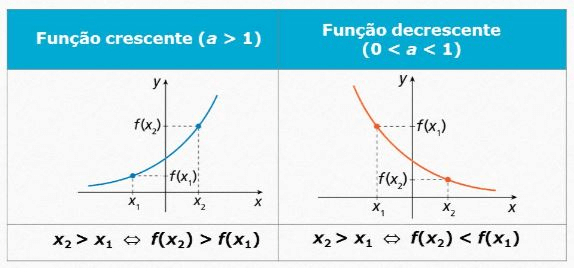 
Essa função é bijectiva, logo, admite função inversa.
Características fundamentais da função exponencial
As características a seguir irão te ajudar a fazer exercícios com funções exponenciais.
- f(1) = a
- f(x1 + x2) = f(x1) . f(x2)
- f(x + h) = ax+h = ax . ah = ah.f(x)
Essas ideias podem ser usadas no estudo de funções exponenciais como f(x) = 2.3x; f(x) = 5x-2; f(x) = 5x -2; e assim por diante.
Reciproca da função exponencial
Dada a função exponencial f definida por f(x) = ax, chamamos de recíproca da função exponencial f a função g, tal que g(x) = a-x. Por exemplo, se f(x) = 2x, sua recíproca será g(x) = 2-x = (1/2)x.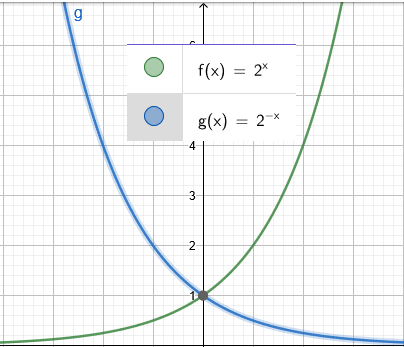
Aplicações da função exponencial
Uma função exponencial muito importante na matemática é aquela cuja base é a constante e, chamada de número de Euler, base dos logaritmos naturais.
A função exponencial de base e é dada por f(x) = ex e aprece em muitas aplicações na matemática, além de descrever diversos fenômenos naturais.
O crescimento exponencial é característico de certos fenômenos naturais. No entanto, de modo geral, não se apresenta na forma ax, mas sim modificado por constantes características do fenômeno: f(x) = C . akx – sendo C e k essas constantes.
Como resolver exercícios de função exponencial?
Para conseguir entender melhor esses exercícios, você deve fazer uma breve revisão de potenciação e de suas propriedades. A seguir, veja na tabela as propriedades das potências:
Além disso, você também pode encontrar exercícios que envolvam raízes. É interessante fazer uma revisão de radiciação.
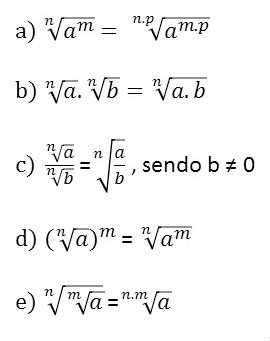
Você pode, ainda, encontrar uma potência com expoente racional, por exemplo, 2½ . Nesse caso, seja am/n , esse número é a raiz n-ésima de am. Portanto, vale dizer que: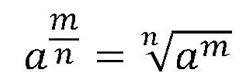
Com real e positivo.
Exercício resolvido
1) (FMJ – SP) O número de bactérias em uma cultura t horas após o início de certo experimento é dado pela expressão:
N(t) = 1 200 . 20,41.t
Nessas condições, quanto tempo após o início do experimento a cultura terá 38.400 bactérias?
RESOLUÇÃO
N(t) = 38 400
Temos que:
38 400 = 1 200 . 20,41.t
20,41.t = 38 400/1200
20,41.t = 32
20,41.t = 25
Portanto:
0,41t = 5
t = 12,5h ou 12h e 30 minutos.
