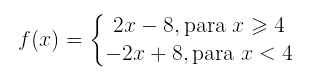Chamamos de função modular a função f(x) = |x|, na qual seu domínio é dado pelos números reais e sua imagem são os números reais positivos. Isso ocorre porque, para todo valor negativo existente no eixo y, a função modular irá fazer com que |-y| = -(-y) = y. Portanto, o gráfico não apresenta reta no terceiro e quarto quadrante.
Os números inteiros são também chamados de números relativos, pois seus valores são determinados em relação ao número zero, que é a origem da reta numerada. Se a posição do número, à direita ou à esquerda do zero, for desconsiderada, tem-se o “valor absoluto” ou “módulo do número”.
Modulo do número real
O módulo do número real r é representado por | r | e é considerado r se r ≥ 0 ou –r se r ≤ 0.
Por exemplo:
- |2| = 2, porque, nesse caso, 2 > 0;
- |-2| = – (-2) = 2, porque –2 < 0.
Resumindo, o módulo de um número na reta real indica a distância desse número ao zero.
Função modular: o que é e como calcular?
Dado um número real x, sempre existe |x| e seu valor é único. Assim, temos uma função de domínio nos números reais e imagem nos números reais positivos, chamada função modular.
Definindo a função modular, temos que: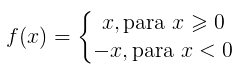
Porém, para trabalharmos melhor com funções modulares, precisamos conhecer as propriedades do módulo.
Propriedades envolvendo módulo
Temos, como consequência da definição de módulo:
- |x| ≥ 0, ∀ x ∈ R;
- |X| = 0 ⇔ X = 0;
- |X| ≥ X, ∀ x ∈ R;
- |X| = |-X|, ∀ x ∈ R.
Considerando isso, podemos encontrar algumas propriedades do módulo para valores de x e y pertencentes aos números reais:
Gráfico da função modular
Podemos construir o gráfico de f(x) = |x| a partir do gráfico de g(x) = x, basta realizar uma reflexão da parte do gráfico de g(x), cujas imagens (valores que assumimos para y) sejam negativas.
A reflexão de um ponto (x, y) em torno do eixo Ox é o ponto (x, -y), assim, os valores de f(x) negativos se tornam positivos, e vice-versa.
No caso dos gráficos de funções modulares do tipo f(x) = |g(x)|, podemos obtê-los fazendo a reflexão da parte do gráfico de g(x), cujas imagens sejam negativas.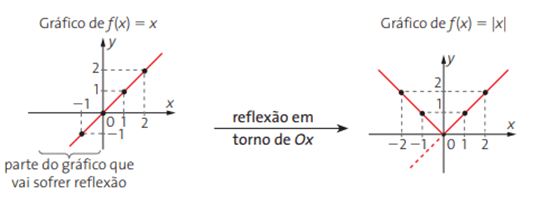
De modo geral, podemos perceber que:
- O gráfico de uma função g(x) = |x| + k é congruente ao de f(x) > |x|, porém transladado para cima (quando k > 0) ou para baixo (quando k < 0). O número de unidades do deslocamento para cima ou para baixo é o valor absoluto de k;
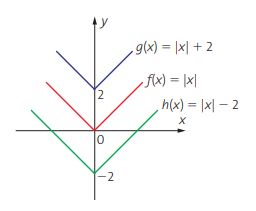
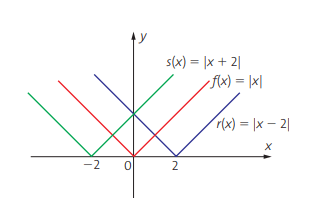
- O gráfico de uma função h(x) = |x – m| é congruente ao de f(x) = |x|, porém transladado para a direita (quando m > 0) ou para a esquerda (quando m < 0). O número de unidades do deslocamento é o valor absoluto de m;
- O gráfico de uma função p(x) = |x – m| + k é congruente ao de f(x) = |x|, porém transladado para a direita ou para a esquerda (quando m > 0 ou m < 0) e para cima ou para baixo (k > 0 ou k < 0). O número de unidades dos deslocamentos são os valores absolutos de m e de k, respectivamente.
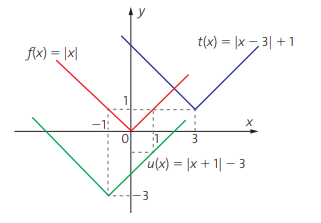
Exercícios resolvidos
1) Dada a função f(x) = |2x – 8|:
A) Calcule f(5), f(1), f(-4) e f(4).
B) Escreva f(x) com sentenças que não têm módulo.
RESOLUÇÃO:
A) f(5) = | 2 . 5 – 8| = |2| = 2
f(1) = |2 . 1 – 8| = |-6| = 6
f(-4) = |2 . (-4) – 8| = |-16| = 16
f(4) = | 2 . 4 – 8| = |0| = 0
B) Primeiro, vamos procurar o ponto onde o gráfico toca o eixo x, que ocorre quando y = 0:
2x – 8 = 0 ⇒ 2x = 8 ⇒ x = 4
Agora, devemos analisar como a função irá se comportar para valores maiores e menores que 4:
X ≥ 4 ⇒ 2x – 8 ≥ 0 ⇒ f(x) = |2x – 8| = 2x – 8
X < 4 ⇒ 2x – 8 < 0 ⇒ f(x) = |2x –8| = -(2x – 8) = -2x + 8
Portanto, podemos escrever a função da seguinte maneira:
