Funções trigonométricas são as funções obtidas pelo círculo trigonométrico. A representação das relações trigonométricas no círculo de raio unitário levou os matemáticos a estudar seu comportamento, esboçando-as graficamente. Assim, essas relações foram identificadas como funções, e foi Gilles Roberval o primeiro a esboçar a curvatura do seno. O estudo dessas funções teve seu ápice com Joseph Fourier, no campo dos movimentos periódicos.
Em várias áreas do conhecimento ocorrem fenômenos periódicos oscilatórios, cujos comportamentos podem ser estudados e compreendidos se forem descritos por meio de funções trigonométricas, por exemplo, seno e cosseno. O movimento harmônico é uma das áreas da física que utiliza funções trigonométricas para descrever um movimento oscilatório e periódico.
Ideia de seno e cosseno de um número real
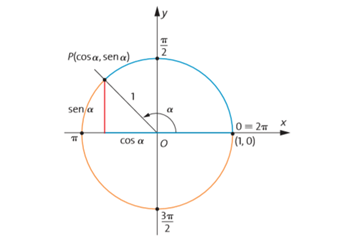
Dada uma circunferência trigonométrica, vamos considerar um ponto P(x, y) pertencente a ela. O ponto P é exatamente o ponto final do arco de circunferência (em azul) de medida α rad.
Lembre-se: medimos arcos de acordo com seus ângulos.
Nessa situação, temos:
- sen α = ordenada de P (valor de x);
- Cos α = abscissa de P (valor de y);
- Tan α = sen α/ cos α.
O eixo das abscissas é também chamado eixo dos cossenos e o eixo das ordenadas é também chamado eixo dos senos.
Ao associar um número real α a um arco da circunferência, estamos associando um número real ao ponto P, cuja abscissa é o cosseno de α e cuja a ordenada é o seno de α. Assim, descrevemos as funções seno e cosseno para todos os números reais.
Isto é, dado um número real x, podemos associar a ele o valor do cosseno ou seno de um ângulo de x (o ângulo x é a medida de um arco da circunferência trigonométrica).
Vamos analisar o seno de um ângulo x. Esse ângulo forma um arco de circunferência que termina no ponto M. O ponto M tem como ordenada o valor do seno desse ângulo x. Portanto, caso quiséssemos montar uma tabela com vários valores de ângulos, como ângulos x = 0°, x = 30° e assim por diante, obteríamos:
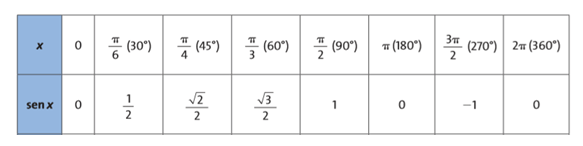
Com esses valores, podemos montar um gráfico que apresente os valores adotados para x e o seno desse ângulo x representado no eixo y, como mostra a figura abaixo:
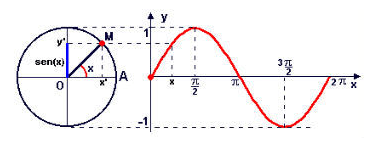
Do mesmo modo, para cada ângulo x (que é a medida de um arco na circunferência trigonométrica), temos um ponto M, que é o final desse arco que possui a abscissa igual ao cosseno do ângulo x. Se representássemos vários valores de ângulo de arcos e as abscissas dos seus respectivos pontos em um gráfico, teríamos:
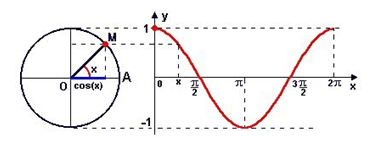
Ou seja, observado os valores que os pontos da circunferência trigonométrica assumem para suas ordenadas e abscissas de acordo com um determinado arco de ângulo θ, temos:
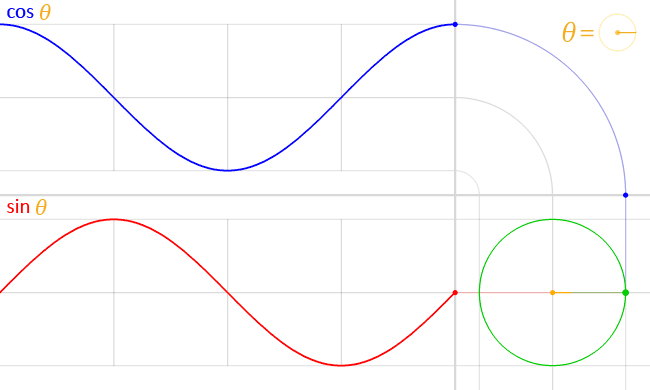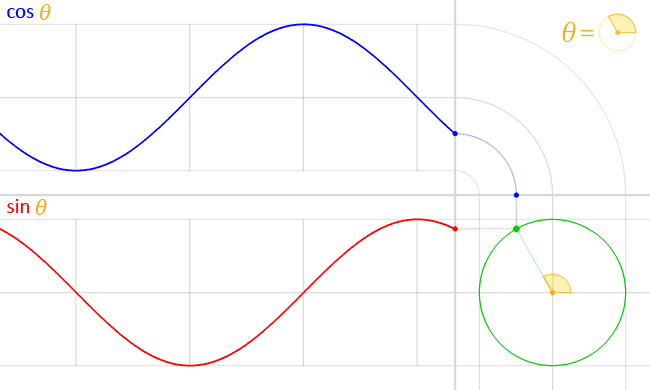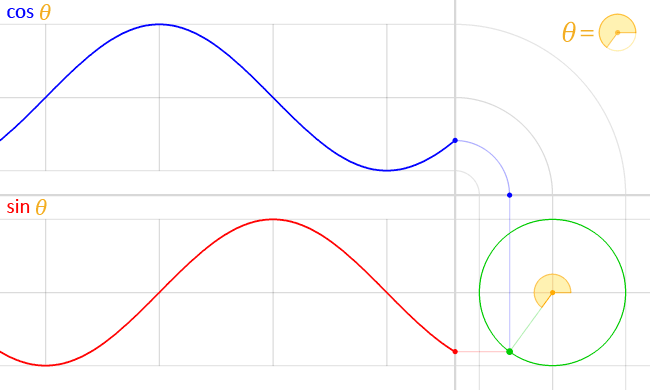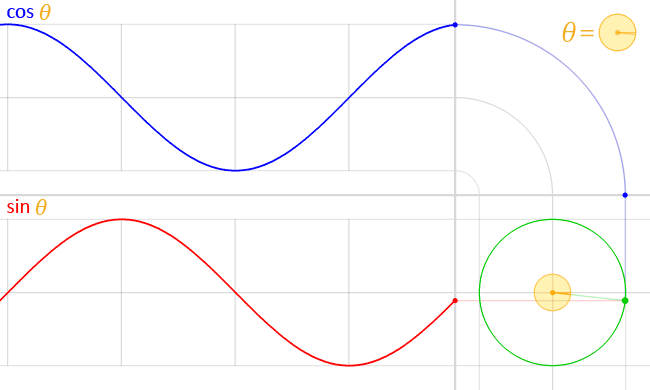
Por fim, definimos a tangente do ângulo x como tan x = senx/cosx, que pode ser obtida graficamente da seguinte maneira:
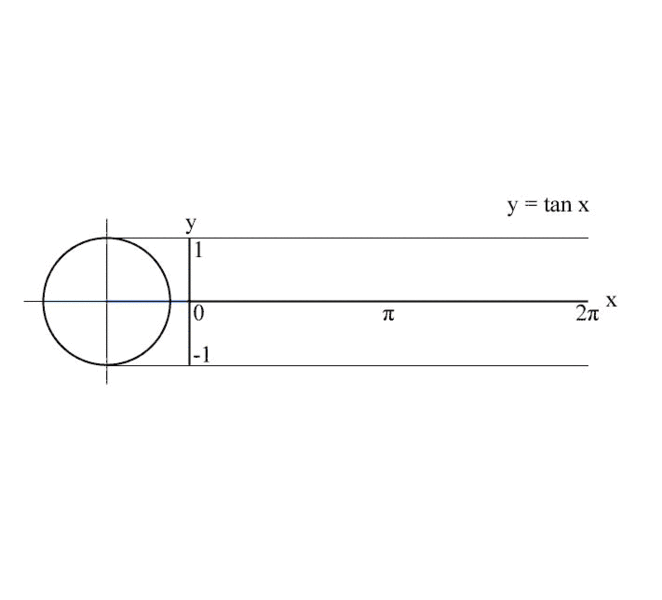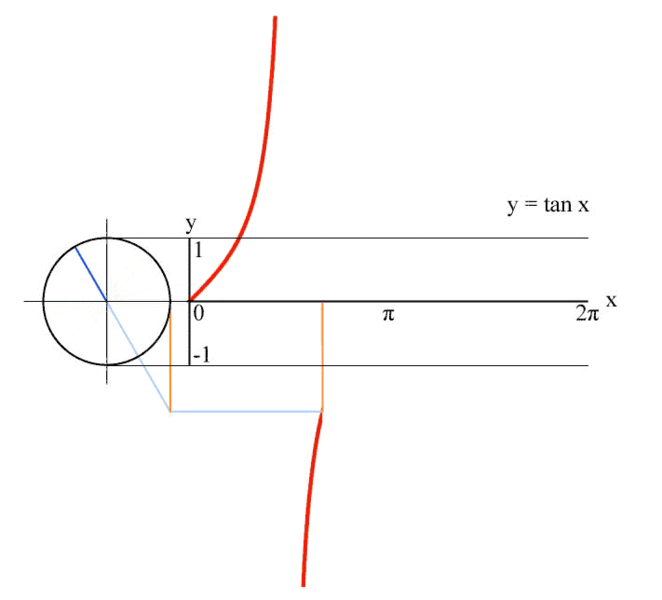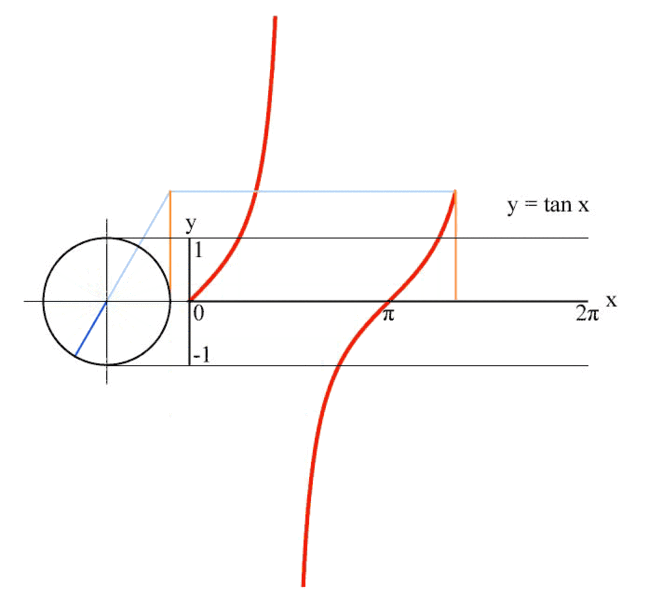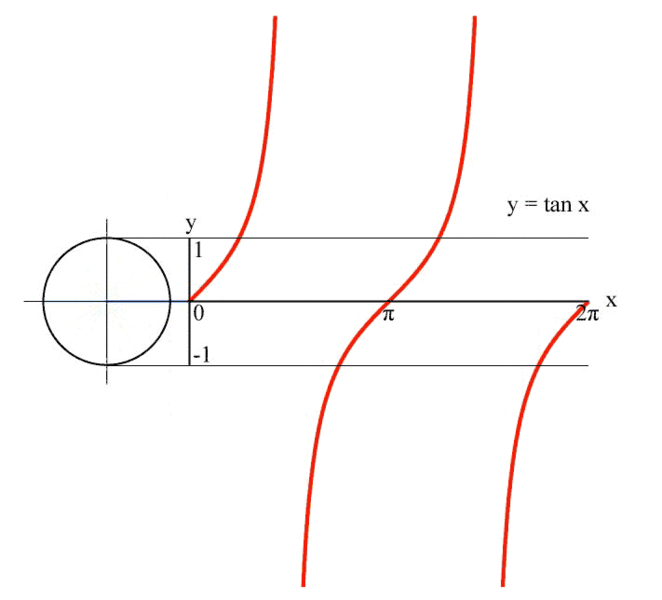
Função seno
Dado um número real x, podemos associar a ele o valor do seno de um ângulo (ou arco) de x radianos.
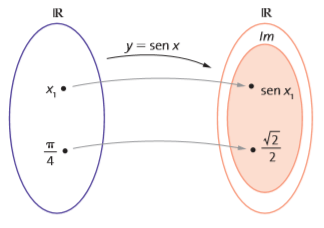
Assim, definimos a função trigonométrica seno como a função real de variáveis reais que associa a cada número real x o valor real sen x, ou seja: F(x) = sen x.
Como a função f(x) = sen x é definida no conjunto dos números reais, ou seja, seu domínio são os números reais R e sua imagem é Im(f) = [-1,1].
O gráfico da função é a curva chamada senoide, que tem o seguinte aspecto:
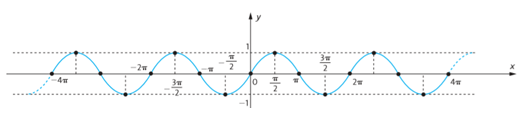
Observando o gráfico da função seno, vemos que a função repete periodicamente seus valores nos intervalos …, [-2π, 0], [0, 2 π], [2 π, 4 π], … Daí dizermos que a função seno é periódica e seu período é igual a 2π.
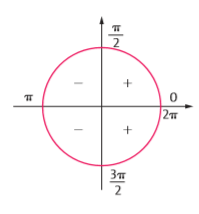
Observando o sinal da função seno, vemos que a função é positiva para valores do 1º e 2º quadrantes e negativa para valores do 3º e 4º quadrantes.
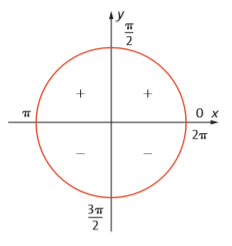
Além disso, a função seno é ímpar, pois sem –x = –sen x para todo x real. Também não é não é injetiva nem sobrejetiva.
Função cosseno
Definimos a função trigonométrica cosseno como a função real de variáveis reais que associa a cada número real x o valor real cos x, ou seja: F(x) = cos x.
O gráfico da função cosseno é a curva chamada cossenoide, que tem o seguinte aspecto:
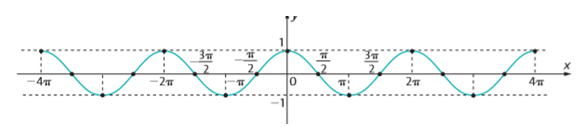
Seu domínio são os números reais e sua imagem é Im(f) = [-1,1], mesma imagem e domínio da função seno.
Também é uma função periódica de período 2π e é uma função par, pois cos(-x) = cos x.
A cossenoide não é uma nova curva, e sim uma senoide transladada π/2 unidade para a direita.
Observando o sinal da função f(x) 5 cos x, vemos que a função cosseno é positiva para valores do 1º e 4º quadrantes e negativa para valores do 2º e 3º quadrantes.
