Geometria analítica – O que é? Conceitos, Fórmulas e Exercícios resolvidos
René Descartes relacionou a álgebra com a geometria em sua obra chamada Discurso do Método, na qual estabeleceu uma relação entre curvas do plano cartesiano e equações algébricas. Assim, o plano cartesiano e as coordenadas cartesianas acabaram recebendo esse nome como homenagem a ele.
A computação gráfica e seu desenvolvimento é um exemplo da aplicação da geometria analítica. Telas de computadores usam estruturas de planos cartesianos com uma quantidade finita de pixels, que determina a resolução das imagens. Conheça, a seguir, um pouco mais sobre a geometria analítica.
Geometria analítica: o que é?
Dividimos o estudo da geometria analítica em três categorias: ponto e reta circunferência, secções e cônicas. A seguir, iremos entender conceitos referentes a ponto e reta.
Conceitos e fórmulas
Distância entre dois pontos
Dado um ponto A de coordenadas (x1, y1) e dado um ponto B de coordenadas (x2, y2), a distância entre eles é dada por: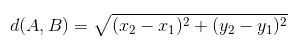
Ponto médio de um seguimento de reta
Dado um seguimento de extremidades A (x1, y1) e B (x2, y2), a abscissa x e a ordenada y do ponto médio é dada por: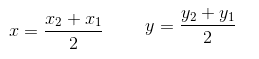
Coordenadas do baricentro de um triângulo
Dado um triângulo ABC de coordenadas A (x1, y1), B (x2, y2) e C (x3, y3), determinamos as coordenadas do baricentro pelas seguintes expressões: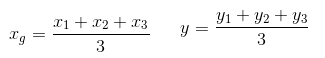
Condição de alinhamento de três pontos
Se três pontos A (x1, y1), B (x2, y2) e C (x3, y3) estão alinhados, então o determinante da matriz que contém as coordenadas deve ser obrigatoriamente igual a zero.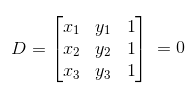 Caso o determinante seja diferente de zero, os três pontos não são colineares.
Caso o determinante seja diferente de zero, os três pontos não são colineares.
Coeficiente angular de uma reta
O coeficiente angular da reta r é o número real m que expressa a tangente trigonométrica de sua inclinação, que é o ângulo que a reta faz com o eixo x.
Sendo α esse ângulo, dizemos que o coeficiente angular pode ser descrito como: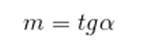 Além disso, conhecendo dois pontos de uma reta, podemos determinar seu coeficiente angular sem conhecer esse ângulo. Sendo os pontos A (x1, y1) e B (x2, y2) pertencentes à reta r, seu coeficiente angular é dado por:
Além disso, conhecendo dois pontos de uma reta, podemos determinar seu coeficiente angular sem conhecer esse ângulo. Sendo os pontos A (x1, y1) e B (x2, y2) pertencentes à reta r, seu coeficiente angular é dado por: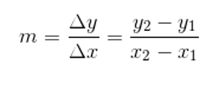
Equações da reta
Considerando o coeficiente angular m da reta e dois pontos pertencentes à mesma, podemos escrever então sua equação. Essa equação pode ser escrita de diferentes modos, veja-os a seguir: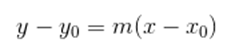 Podemos ainda escrever a equação da reta na forma reduzida. Para montar essa equação, é preciso escolher o ponto em que a reta intersecta o eixo y, de coordenada (0, n). Chamamos esse número n de coeficiente linear e junto com o coeficiente angular, podemos montar essa equação da reta.
Podemos ainda escrever a equação da reta na forma reduzida. Para montar essa equação, é preciso escolher o ponto em que a reta intersecta o eixo y, de coordenada (0, n). Chamamos esse número n de coeficiente linear e junto com o coeficiente angular, podemos montar essa equação da reta.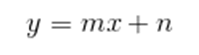 Além disso, podemos utilizar a equação geral da reta:
Além disso, podemos utilizar a equação geral da reta: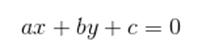 As letras a, b e c representam constantes. Para escrever a equação de uma reta dessa maneira, observe o exemplo abaixo:
As letras a, b e c representam constantes. Para escrever a equação de uma reta dessa maneira, observe o exemplo abaixo:
Y – 3 = 5(x – 1) pode ser escrita da seguinte maneira:
Y – 3 = 5x –5
5x – y –2 = 0
Distância entre um ponto e uma reta
Para achar a distância entre uma reta r de equação ax + by + c = 0 e um ponto P (xp, yp), usamos a seguinte expressão: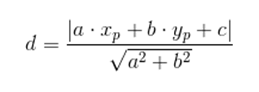
Ângulo formado por duas retas
Vamos considerar duas retas concorrentes r e s, não perpendiculares entre si, e que possuem coeficientes angulares m1 e m2. Podemos calcular o ângulo entre elas a partir da seguinte fórmula: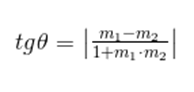 Para encontrar o ângulo, calcule o arc tg do valor obtido pela expressão acima. Você pode usar uma calculadora para isso.
Para encontrar o ângulo, calcule o arc tg do valor obtido pela expressão acima. Você pode usar uma calculadora para isso.
Se as retas são paralelas, os coeficientes angulares são iguais. Ou seja: m1 = m2. Se forem retas perpendiculares, m1. m2 = -1.
Área de uma região triangular
Dado um triângulo ABC de vértices A (x1, y1), B (x2, y2) e C (x3, y3), podemos calcular a sua área pela seguinte expressão: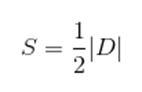 Sendo D o determinante da seguinte matriz, formada pelas coordenadas dos vértices A, B e C desse triângulo.
Sendo D o determinante da seguinte matriz, formada pelas coordenadas dos vértices A, B e C desse triângulo. 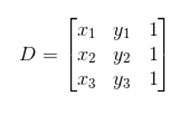 Lembre-se: o valor do determinante está em módulo, portanto, considere sempre valores positivos.
Lembre-se: o valor do determinante está em módulo, portanto, considere sempre valores positivos.
Caso você não se lembre como é o cálculo do determinante de uma matriz, veja o vídeo a seguir:
Exercícios resolvidos
1) Determine a área de uma região triangular ABC, dados os pontos A ( -1, 2), B (3,1) e C (2,0).
Primeiramente, vamos calcular o determinante com as coordenadas dos vértices desse triângulo: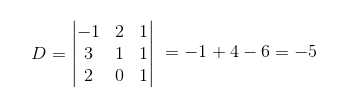 Agora, vamos colocar esse valor na expressão que calcula a área.
Agora, vamos colocar esse valor na expressão que calcula a área.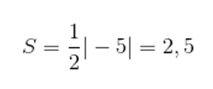







Deixe seu comentário