Homotetia é o processo utilizado para ampliar ou reduzir figuras a partir de um ponto fixo.
Há vários mecanismos para se obter figuras semelhantes, tais como máquinas copiadoras e ampliação de fotos. A homotetia é um recurso que usamos para ampliar figuras com instrumentos de desenho.
Esse processo utiliza um ponto O, chamado polo, e uma constante de proporção, chamada razão de semelhança k. Ao realizar uma ampliação ou redução por homotetia, são mantidos:
- Ângulos;
- Razões de semelhança k entre os lados das figuras;
- Paralelismo entre os lados do polígono ampliado ou reduzido.
Como ampliar ou reduzir polígonos por homotetia?
Primeiramente, marque um ponto fixo O (polo). Em seguida, trace as semirretas que liguem o ponto O a cada um dos vértices do polígono, como na imagem abaixo.
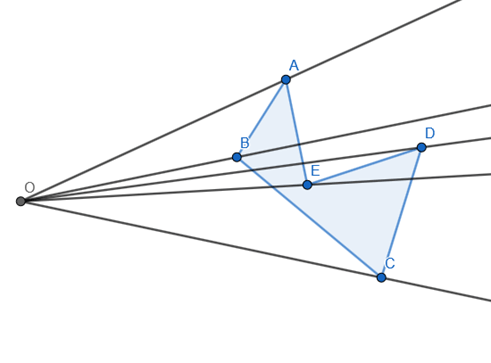
Agora, marque os novos pontos do polígono ampliado, respeitando a constante de ampliação. Por exemplo: ao realizar uma duplicação do polígono ABCDE da imagem acima, iremos obter um novo polígono A’B’C’D’E’.
Para isso, iremos descobrir a medida dos seguimentos AO, OB, OC, OD e OE. Em seguida, se quisermos duplicar o polígono, devemos traçar um novo seguimento OA’ com o dobro do tamanho do seguimento OA, como mostra a figura abaixo:
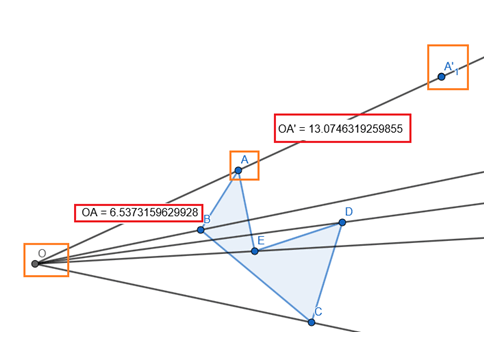
Perceba que o ponto A’ foi marcado exatamente em cima do seguimento que contém o ponto A – AO = 2 . OA’.
Resta fazer o mesmo com os outros pontos B, C, D e E do polígono:
- Descubra a distância dos seguimentos OB, OC, OD e OE. Trace os seguimentos OB’, OC’, OD’ e OE’ de modo que:
OB = 2 . OB’
OC = 2 . OC’
OD = 2 . OD’
OE = 2 . OE’
Ou seja, de modo que os novos seguimentos tenham a medida igual ao dobro do seguimento antigo.
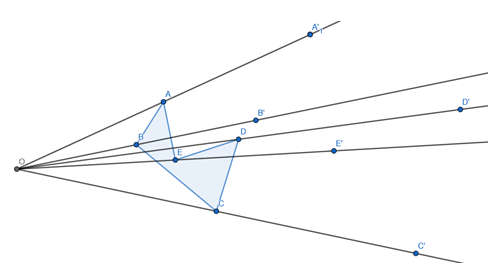
Por fim, basta ligar os novos pontos obtidos: ligue A’ com B’, B’ com C’, e assim por diante.
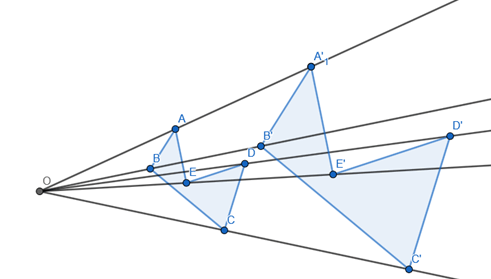
Com isso, o novo polígono obtido A’B’C’D’E’ será uma ampliação do polígono ABCDE.
No exemplo acima, fizemos a ampliação do polígono ABCDE, obtendo um novo polígono A’B’C’D’E’. O tamanho do seguimento OA’ é o dobro do seguimento AO, como vimos acima: OA’ = 2 . AO.
O número que multiplicamos os seguimentos OA, OB, OC, OD e OE para obter os novos seguimentos OA’, OB’, OC’, OD’, e OE’ é chamado de constante de proporcionalidade k.
Isto é: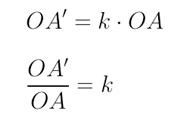
Essa constante nos auxilia no processo de homotetia e nos garante a relação entre a medida dos lados das figuras durante a ampliação ou redução.
Como a constante de proporcionalidade é k = 2, os lados do polígono A’B’C’D’E’ terão o dobro dos lados correspondentes do polígono ABCDE, isto é, o seguimento A’B’ tem o dobro da medida do seguimento AB: A’B’ = 2 . AB. Isto é: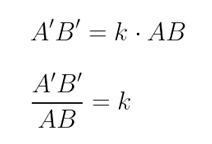
Dica: Lados e ângulos correspondentes são os que estão na mesma posição relativa nos dois polígonos.
Propriedades de figuras semelhantes
O resultado do processo de homotetia em polígonos são dois polígonos semelhantes dispostos, isto é, na mesma posição relativa.
Dois polígonos são semelhantes quando satisfazem as duas condições:
- As medidas dos lados que se correspondem são proporcionais;
- As medidas dos ângulos que se correspondem são iguais.
Sendo ABCD um polígono e A’B’C’D’ sua ampliação.
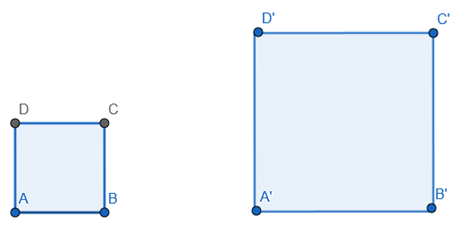
Os lados correspondentes se relacionam a partir de uma constante chamada razão de semelhança k. Isto é, ao multiplicar a medida de um dos lados do polígono ABCD por k, você encontrará a medida do lado correspondente de sua ampliação. Ou seja: A’B’ = AB . K.
Com isso, podemos estabelecer uma relação entre os lados correspondentes e a constante de proporcionalidade: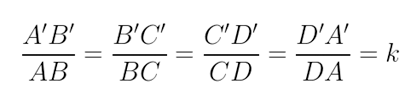
Ou seja, a divisão entre dois lados correspondentes de polígonos semelhantes obtidos por meio de homotetia sempre resultará na constante de proporcionalidade k.
Resumindo, a constante de proporcionalidade pode ser obtida em dois momentos:
- Fazendo a divisão entre os lados correspondentes do polígono e sua ampliação/redução;
- Fazendo a divisão entre o seguimento que liga o ponto fixo (polo) O e o vértice do polígono pelo seguimento que liga o ponto O ao vértice correspondente da ampliação.
Além disso, os ângulos correspondentes das duas figuras permanecem os mesmos (são congruentes). Observe dois ângulos correspondentes de iguais medidas na imagem abaixo: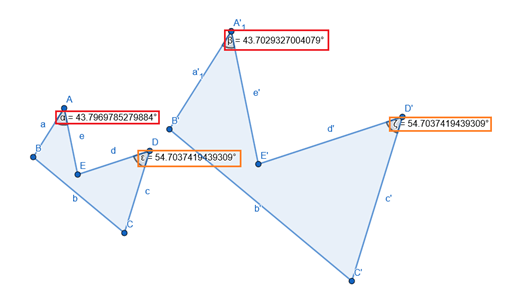
Além disso, a área do polígono A’B’C’D’E’ possui relação com a área do polígono ABCDE.
Sendo A1 a área do polígono original e A2 a área de sua ampliação ou redução, a relação entre elas será: 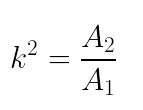
No exemplo abaixo, a área do polígono ABCD é A1 = 4 cm². A área de sua ampliação A’B’C’D’ é A2 = 16 cm². A razão de semelhança entre as duas figuras será:
K² = A2/A1
K² = 16/4
K² = 4
K = 2.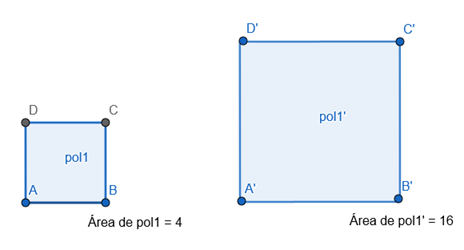 O perímetro de figuras ampliadas também possui relação. Sendo P1 o perímetro do polígono ABCD, o perímetro P2 de sua ampliação é dado por: P2 = k . P1
O perímetro de figuras ampliadas também possui relação. Sendo P1 o perímetro do polígono ABCD, o perímetro P2 de sua ampliação é dado por: P2 = k . P1
Por exemplo: um quadrado de lado l = 2cm possui um perímetro P1 = 8cm. Foi realizada uma ampliação desse quadrado que gerou uma nova figura, de perímetro P2 = 24cm. A razão de semelhança entre os dois quadrados será: P2 = k . P1.
P2/P1 = k
K = 24/8
K = 3

