Lei de Ohm – O que é? Para que serve? Exemplos Resolvidos
O físico George Ohm observou que, quando variava a tensão nas extremidades de um resistor, a intensidade da corrente variava proporcionalmente, se a temperatura do sistema fosse mantida constante.
Essa observação pode ser escrita em linguagem matemática da seguinte maneira: V = R i; em que V é a tensão e i à corrente elétrica.
A constante de proporcionalidade R é a resistência elétrica do resistor. Nas unidades SI, R deve ser dada em (Volt/Ampère), mais conhecida como ohm.
Geralmente, essa unidade é denotada pela letra grega ômega maiúscula (Ω), em uma homenagem a Georg Simon Ohm.

O múltiplo quilo-ohm (kΩ), mil vezes maior que o ohm, costuma ser usado com certa frequência.
Observe a seguinte relação: 1kΩ = 1000Ω = 103Ω
Exemplo:
- Quanta corrente fluirá por uma lâmpada com 60Ω de resistência quando 12 V de voltagem forem aplicados a ela?
Solução
- Qual é a resistência de uma torradeira sujeita a uma corrente de 12A quando conectada a uma tomada de 120 V?
Solução
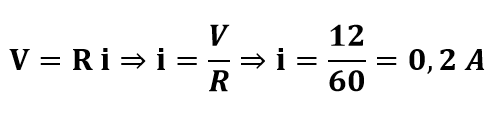
Resistores ôhmicos
Os resistores que obedecem à 1a Lei de Ohm são denominados resistores ôhmicos. É o caso da maioria dos condutores metálicos.
O gráfico de V x I de um resistor é conhecido como a sua curva característica. No caso de resistores ôhmicos, as curvas devem se assemelhar ao gráfico, abaixo.
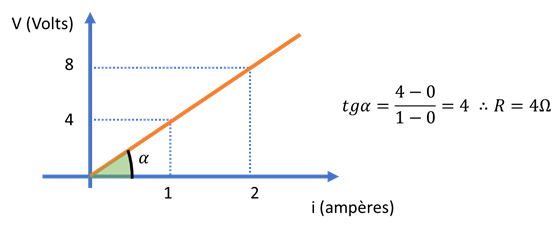 Para esses casos, a curva característica é uma reta que passa pela origem. A declividade da reta é constante e vale R. Como exemplos de materiais mais comuns podemos citar: ferro, cobre, alumínio, prata, outro, liga de níquel-cromo, etc.
Para esses casos, a curva característica é uma reta que passa pela origem. A declividade da reta é constante e vale R. Como exemplos de materiais mais comuns podemos citar: ferro, cobre, alumínio, prata, outro, liga de níquel-cromo, etc.
Exemplo
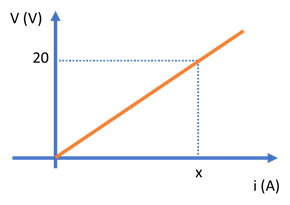
A figura representa o gráfico tensão x corrente de um resistor de 100Ω. O valor de x, em A é de:
a) 100
b) 20
c) 2
d) 0,5
e) 0,2
Solução:
Sabemos que:
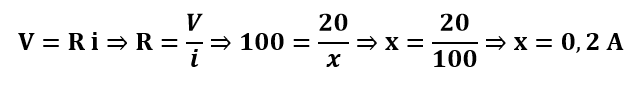
A letra correta é “e”.
Resistência em função das dimensões do fio (2a Lei de Ohm)
As experiências de Ohm nos permitem concluir que:
- Para um mesmo material, o valor da resistência elétrica de um fio é diretamente proporcional ao seu comprimento. Veja um exemplo:
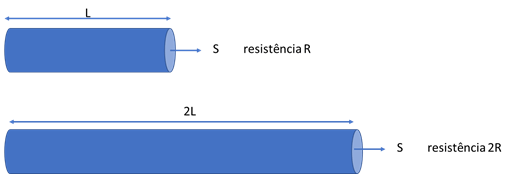
- Para um mesmo material, o fio de mesmo comprimento que tiver a maior secção reta tem resistência elétrica menor. Veja um exemplo:
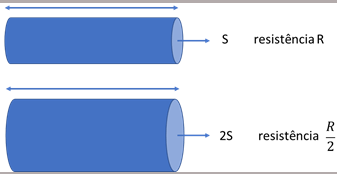
A resistência elétrica de um fio é diretamente proporcional ao seu comprimento, inversamente proporcional à área de sua secção reta e depende do material do qual o fio é feito.
A expressão que leva em conta todas essas características é dada pela fórmula a seguir:
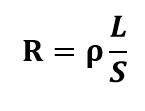 Em que L é o comprimento do fio, S a área de sua secção reta, e ρ é uma constante de proporcionalidade característica do material, chamada resistividade. Nas unidades SI, ρ é dada em Ω.m.
Em que L é o comprimento do fio, S a área de sua secção reta, e ρ é uma constante de proporcionalidade característica do material, chamada resistividade. Nas unidades SI, ρ é dada em Ω.m.
Exemplo:
Calcule a resistência elétrica de um fio de 40m de comprimento, de 2mm2 de secção transversal, sendo a resistividade de cobre igual a 1,710-8 Ω.m.
Resolução:
O primeiro passo consiste em retirar as informações do enunciado:
L = 40 m
S = 2 mm2 = 2.10-6 m2
ρ =1,710-8 Ω.m.
R = ?
Em seguida, substituímos na expressão para o cálculo da resistividade:
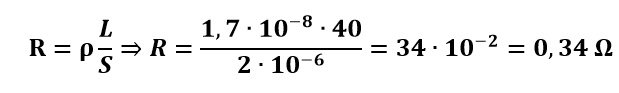
Condutores não ôhmicos
Os resistores para os quais não é válida a lei de Ohm são denominados resistores não ôhmicos. Como exemplo, podemos citar carbono, germânio e silício. Nestes, a tensão V não é proporcional à intensidade da correte i, o que significa dizer que a resistência elétrica R não permanece constante.
Para cada V há um valor diferente de resistência elétrica. Representando graficamente a tensão V em função da intensidade da correte i, para resistores não ôhmicos, obtemos uma reta que passa pela origem do sistema de eixos.
Para os resistores não ôhmicos, obtemos uma curva que passa pela origem dos eixos, não uma reta.
Potência elétrica
A potência elétrica que se dissipa num resistor pode ser calculada pela equação P = V . i. Nesse caso, pode-se substitui V pela lei de Ohm, de tal modo obtermos: P = V.i = R.i.i = R.i2.
Para o resistor ôhmico, cuja resistência elétrica é constante, podemos concluir, em vista dessa equação, que:
A potência elétrica dissipada num resistor ôhmico é diretamente proporcional ao quadrado da intensidade de corrente.
Em P = V.i, podemos substituir a intensidade de corrente i pela relação i = v/R’, obtendo:
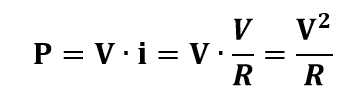
A potência elétrica dissipada num resistor ôhmico é diretamente proporcional ao quadrado da tensão V entre seus terminais.
Exemplo:
Qual a potência em um circuito simples de uma resistência de 5Ω quando submetida a uma tensão de 30V?
Resolução
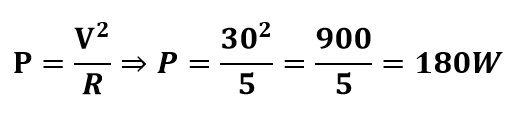






Deixe seu comentário