A lei dos cossenos relaciona as medidas dos três lados de um triângulo e o cosseno de um dos ângulos.
Quando usar a Lei dos Cossenos?
Como a lei fornece uma relação entre os três lados e o cosseno de um dos ângulos, quatro medidas, basta utilizá-la quando falta uma dessas informações e você possui as outras três.
Em contrapartida, a lei dos senos fornece uma relação entre cada lado e cada seno do ângulo, em pares. Então, se você tiver o valor de dois lados de um triangulo e um ângulo e precisar achar o outro, então é a lei dos senos que deverá ser utilizada.
Fórmula da lei dos cossenos
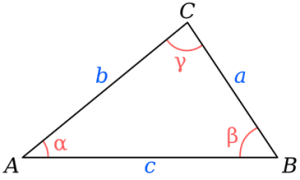
Na figura acima, temos a representação de três lados: a, b e c. Também temos os ângulos α, ? e γ. A lei pode ser escrita da seguinte forma:
a2=b2+c2 -2.b.c.cos α
Repare que o lado “a” ao quadrado tem que ser igual à soma dos quadrados dos outros dois lados menos duas vezes o produto desses lados multiplicado pelo cosseno do ângulo que está do lado oposto de “a”. Essa mesma ideia pode ser aplicada para os outros lados também, mas repare que estamos escrevendo a mesma ideia, só que para incógnitas diferentes!
b2=a2+c2 -2.a.c.cos β
c2=a2+b2 -2.a.b.cos γ
Exemplos de aplicação
1. Considere um triângulo que possui lados a = 8 e b = 9 e um ângulo =60°. Qual o tamanho do lado c?
Solução: Percebemos que temos o ângulo γ, então precisamos selecionar a lei que possui esse ângulo:
c2=a2+b2 -2.a.b.cos γ
Substituindo os valores, temos:
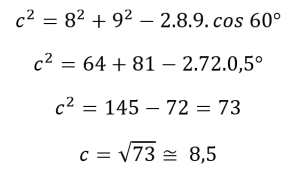
2. Se temos um triangulo com lados a = 10, b = 11 e c = 9, qual o valor do ângulo α?
Solução: Utilizamos a primeira relação:
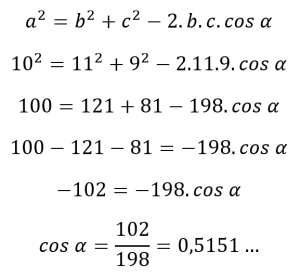
Aqui precisamos encontrar o ângulo cujo cosseno vale 0,5151… Para isso usamos a função inversa do cosseno, o arco cosseno, que pode ser escrita como cos-1(x) ou arccos (x).
![]()
Você também pode gostar de ler:
Média Aritmética – Definição, Tipos e Exemplos
Referência
LANG, Serge. Basic mathematics. Frank Brothers, 1988.

