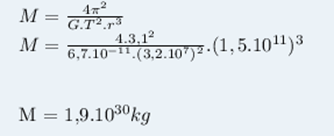A regularidade de certos fenômenos, como os dias, as noites, o nascer do sol, as fases da lua, os eclipses, entre outros eventos, fizeram com que cientistas concluíssem que os corpos celestes se organizavam de alguma forma, a ponto de comporem um grande sistema.
Kepler analisou os dados do astrônomo Tycho Brahe e formulou suas três leis, que tratam do movimento planetário. Quer saber como elas funcionam? Confira essas e outras informações a seguir, só no Gestão Educacional!

Sistemas planetários
Primeiramente, surgiu a ideia de que o Sol e a Lua, como os demais astros, giravam em torno da Terra, pois o sol e a lua desaparecem de um lado e reaparecem do outro e as estrelas e constelações fazem trajetórias circulares.
Porém, era difícil explicar, a partir dessa perspectiva, o movimento de planetas visíveis a olho nu (Mercúrio, Vênus, Marte, Júpiter e Saturno). O primeiro sistema planetário foi o Sistema Geocêntrico, que, embora cheio de imperfeições, foi aceito por 14 séculos.
No século XVI, o astrônomo Nicolau Copérnico propôs o Sistema Heliocêntrico, no qual o Sol ocupava o centro do universo. A Terra seria um dos planetas que girava em torno do astro, em órbita circular (translação) e em torno de si próprio (rotação).
[CLIQUE AQUI PARA MAIS INFORMAÇÕES SOBRE O SISTEMA SOLAR]
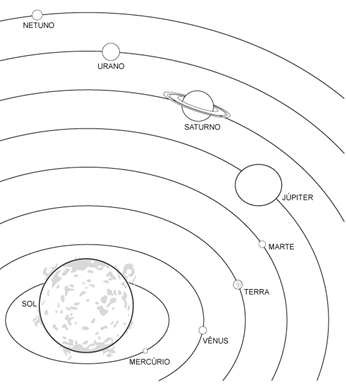
O sol então está fixo no centro do universo e ao seu redor estão todos os planetas. Ele segue o esquema abaixo:
O que são as Leis de kepler?
As suas três leis seguem o modelo heliocêntrico e são as seguintes:
- As órbitas dos planetas são elípticas e o Sol se localiza em um dos focos;
- Os seguimentos de reta traçados do Sol a qualquer planeta (raio vetor) descreve áreas iguais em tempos iguais;
- Os quadrados dos períodos de translação dos planetas são proporcionais aos cubos dos semieixos maiores de suas órbitas.
[VEJA TAMBÉM: QUAIS OS PLANETAS DO SISTEMA SOLAR?]
Primeira lei
Ao contrário do que sempre foi proposto, Kepler afirmou que as órbitas dos planetas não eram circunferências, algo que acabou não agradando a todos, pela falta de simetria, pois o sol ocupava um dos focos da elipse, enquanto o resto era simplesmente preenchido com vácuo.
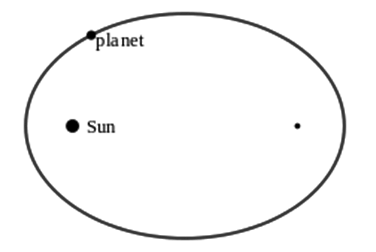
A distância de um dos focos até o objeto, somada a distância do objeto até o outro foco, é sempre igual.
Observe a imagem, abaixo, para imaginar como seria a descrição da primeira lei.
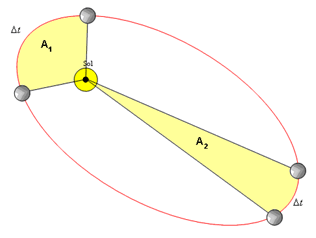
Segunda lei
Essa lei afirma que se as áreas A1 e A2 são iguais as variações de tempo Δt também são iguais.
Os planetas, portanto, se movem com velocidades diferentes, dependendo da distância que eles estão do Sol.
Chamamos de periélio o ponto mais próximo do Sol, no qual o planeta orbita mais rapidamente, ou seja, tem movimento acelerado, atingindo sua Velocidade Máxima (Vmax).
De modo análogo, afélio é o ponto mais afastado do Sol, onde o planeta move-se mais lentamente, o que chamamos de movimento retardado, possuindo sua Velocidade Mínima (Vmin).
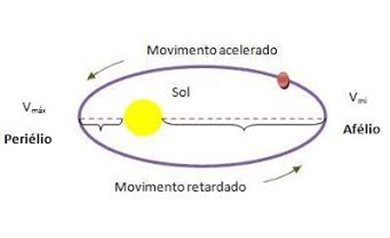
No caso da Terra, o afélio ocorre em junho, quando a terra está a aproximadamente 152 milhões de quilômetros do Sol. Enquanto isso, o periélio ocorre em janeiro, quando a Terra está a 147 milhões de quilômetros do Sol.
Terceira lei
A Terceira lei, também chamada de Lei dos Períodos, determina que o quadrado do período de revolução (T²) de cada planeta em torno do Sol é diretamente proporcional ao cubo da distância média (r³) desse planeta ao sol.
Em termos matemáticos, essa lei pode ser expressa por: T² = K.r³, sendo K uma constante de proporcionalidade.
Lembre-se que o período de revolução é o tempo que um planeta demora para dar uma volta completa em torno do Sol.
Terceira lei e velocidade orbital
As elipses que descrevem as trajetórias dos planetas têm excentricidades muito mais próximas de 0 do que de 1. São praticamente circulares!
A excentricidade da Terra tem medida igual a 0,017, sendo um dos planetas de órbitas mais circulares.
Portanto, embora elípticas, as órbitas dos planetas podem ser consideradas, com boa aproximação, circunferências.
Dessa forma, podemos estudar o movimento dos planetas de forma aproximada e determinar os valores de k de cada planeta.
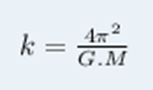
Com isso, podemos apresentar outra expressão para a Terceira Lei de Kepler:
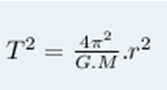
Sendo T o período de revolução do planeta, r o raio médio da órbita, M a massa do Sol e G a constante da gravitação universal, ou seja, G = 6,67 . 10-¹¹ N.m² / kg².
Considerando que a velocidade dos planetas seja uniforme, conseguimos ainda montar a expressão matemática que apresenta o que chamamos de velocidade orbital:
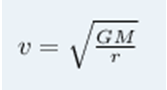
Exercícios Resolvidos
1) O raio médio da órbita da Terra é de 1,5.10¹¹m e o da órbita de Júpiter é de 7,8.10¹¹m. Qual o período de revolução de Jupter em anos terrestres?
SOLUÇÃO:
Para evitar o cálculo de K, podemos aplicar a Terceira Lei de Kepler para a Terra e para Júpiter e dividimos membro a membro as duas equações. Com isso, cancelamos k e determinamos Tj.
1² = k.(1,5.10¹¹)³
Tj² = k.(7,8 . 10¹¹)³
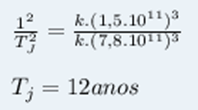
2) Determine a massa do Sol sabendo que o período de revolução da Terra em torno dele é de 1 ano e o raio médio da órbita terrestre é rt = 1,5.10¹¹m.
SOLUÇÃO:
Para obter a massa do sol em quilogramas, precisamos calcular o período de revolução da Terra em torno do Sol em segundos.
Vamos adotar que o dia tem 86.000 segundos e o ano tem 370 dias: T = 370.86.000 = 3,2.10^7s.
Da expressão da Lei de Kepler, faremos: