A lógica matemática estuda as aplicações lógicas na área da matemática para distinguir um raciocínio correto do incorreto. Também conhecida como lógica proposicional ou logica simbólica clássica, essa área de estudo verifica se os argumentos usados em demonstrações ou certas afirmações são verdadeiros.
Assim, é possível fazer a correção ou incorreção de todos os raciocínios matemáticos, para usarmos sempre argumentos válidos. A validação de argumentos ajuda a construirmos a teoria da matemática com proposições logicamente válidas. A seguir, conheça as noções de lógica, só aqui, no Gestão Educacional!
Proposição
Chamamos de proposição toda oração ou sentença que pode ser classificada como verdadeira ou falsa.
Ou seja, tem sujeito e predicado, é declarativa e só tem um valor lógico: ou é verdadeira ou é falsa.
Exemplos podem ser:
- Nove é diferente de cinco. Essa é uma proposição verdadeira.
- Três é divisor de 11. Essa é uma proposição falsa.
Negação
A partir de uma proposição p qualquer, podemos construir a negação de p, que tem como símbolo ~p.
Veja o seguinte exemplo:
- p: nove é diferente de cinco.
- ~p: nove é igual a cinco.
Ou seja, a proposição ~p tem sempre o valor oposto de p, isto é, verdadeira quando p é falsa e falsa quando p é verdadeira.
Podemos montar a seguinte tabela verdade: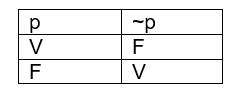
Conectivos
A partir de proposições dadas, podemos construir novas usando símbolos lógicos chamados conectivos: o conectivo ^ (lê-se: e) e o conectivo v (lê-se: ou).
Conectivo ^
A conjunção p ^q é verdadeira se p e q são ambas verdadeiras; se ao menos uma delas for falsa, p^q é falsa.
Usamos a tabela verdade: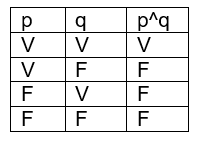
Veja um exemplo:
- p: um quadrado de lado a tem diagonal 2a (F).
- q: um quadrado de lado a tem área a² (V).
- p ^ q : um quadrado de lado a tem diagonal 2a e área a² (F).
Conectivo v
A disjunção p v q é verdadeira se ao menos uma das proposições p ou q é verdadeira. Se p e q são ambas falsas, então p v q é falsa.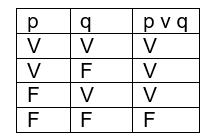
Exemplo:
- p: 10 é número primo (F).
- q: 10 é número composto (V).
- p v q: 10 é primo ou composto (V).
Condicionais
Colocando os condicionais entre duas proposições, obtemos uma nova proposição. A seguir, estão as descrições dos outros símbolos lógicos usados:
Condicional →
O condicional → é usado para formar uma nova proposição: p → q (lê-se “se p então q). Esse condicional é falso somente quando p é verdadeira e q é falsa; caso contrário p → q é verdadeiro.
Resumindo, temos a seguinte tabela verdade: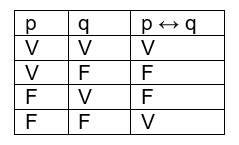
Existe um truque fácil para memorizar condicionais:
- p: chuva;
- q: molhar.
Vamos agora pensar se a chuva e o fato de molhar é (V) ou (F):
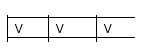
- Se choveu, molhou, isso é verdade (Primeira linha da tabela verdade).
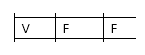
- Se choveu e não molhou, é falso (segunda linha).
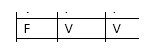
- Se não choveu e molhou, pode ser verdade (terceira linha).
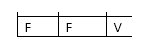
- Se não choveu e não molhou, é verdade (quarta linha).
Condicional ↔
O condicional ↔ entre duas proposições gera uma nova proposição: p ↔ q (lê-se: se p, então q).
A tabela verdade dessa condicional é dada por:Tudo o que foi explicado até agora teve o intuito de construirmos uma tabela verdade posteriormente em exercícios. Caso você ainda tenha dúvidas sobre como preencher uma tabela verdade, assista o seguinte vídeo:
Tautologia
Quando usamos conectivos, modificadores ou condicionais, geramos uma nova proposição. Dizemos que uma proposição é uma tautologia ou proposição logicamente verdadeira quando ela possui apenas o valor lógico verdadeiro, como mostra a parte destacada na imagem abaixo: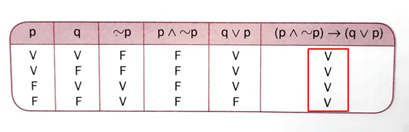
Proposição logicamente falsa
Uma nova proposição gerada pelo uso de conectivos, modificadores ou condicionais é logicamente falsa quando possui apenas o valor lógico falso, como mostra a parte destacada da imagem abaixo: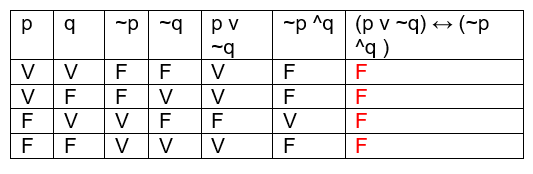
Relação de implicação
Na tabela verdade, quando a proposição final (geralmente última coluna tabela verdade) gerada pela condicional → (se… então…) for uma tautologia, temos uma relação de implicação.
Veja o exemplo:
Mostre que (p ^ q) ⇒ p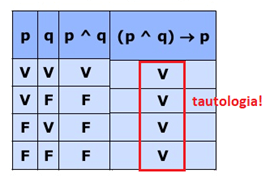
Como (p ^ q) → p é uma tautologia, então (p ^ q) ⇒ p. Isto é, ocorre a implicação lógica.
Todo teorema é uma implicação da forma hipótese ⇒ tese. Assim, demonstrar um teorema significa mostrar que não ocorre o caso de a hipótese ser verdadeira e a tese falsa.
Relação de equivalência
Dadas duas proposições, dizemos que uma é equivalente a outra quando elas possuem tabelas verdade iguais, ou seja, possuem o mesmo valor lógico.
Observe o exemplo abaixo: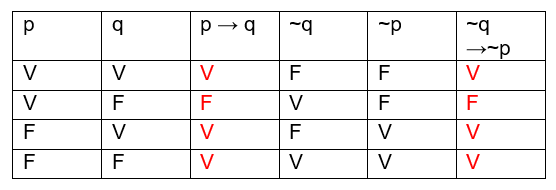
Perceba: as duas colunas destacadas em vermelho são iguais. Portanto: (p → q) ⇔ (~q → ~p).
Todo teorema cujo recíproco é verdadeiro é uma equivalência, pois hipótese ⇔ tese.
