Imagine que a sala onde você estuda realizou uma prova. Todos dizem que foram mal. Então você decide comparar o desempenho da sua sala nessa prova com outra sala. Você irá se deparar com várias notas diferentes. Então como dizer que uma sala foi melhor que outra? Nesse caso, fazemos uma média: uma forma de encontrar um número que representa um conjunto de outros números.
A média aritmética pode ser dividida em média aritmética simples e média aritmética ponderada.

Média aritmética simples
É calculada somando todos os x valores e dividindo pela quantidade n de valores somados.
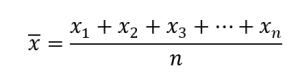
Por exemplo, se quiser calcular a altura média em sua casa, você irá somar as alturas e dividir pelo número de pessoas:
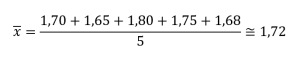
Média aritmética ponderada
A diferença da média aritmética simples é que, dessa vez, teremos números repetidos. Quando isso ocorre, podemos resumir os números repetidos como uma multiplicação desses números.
Por exemplo, suponha que queira encontrar a média entre os números 4, 4, 4, 5, 5, 6, 6, 6 e 6. Note que o número quatro aparece três vezes, o número cinco aparece duas vezes e o número seis aparece quatro vezes. A quantidade que um número aparece denominamos peso k. Então, se somarmos os pesos, teremos a quantidade de números.
Se fizermos a média aritmética simples, teremos:
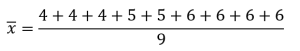
Podemos resumir como:
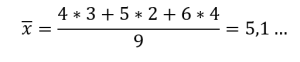
Repare que, se somarmos os pesos 3+2+4, obteremos o divisor 9.
Assim, a média aritmética ponderada possui a seguinte fórmula:
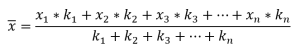
A média ponderada é muito utilizada ao atribuir uma maior nota em certas questões de uma prova, por exemplo, atribuindo um peso maior nas questões mais difíceis e um peso menor nas questões mais fáceis.
Suponha que haja uma prova de cinco questões onde as três primeiras questões têm peso dois e as duas últimas tem peso um, ou seja, a soma dos pesos será 9 (4*2+1*1). Cada questão correta por inteiro é atribuída um valor 10. Se for uma questão em que o aluno acerte só metade, atribuirá-se um valor de 5 etc.
No caso de o aluno acertar todas inteiras, a média será:
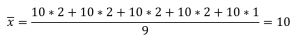
Agora, e se o aluno errar a primeira, acertar por inteiro a segunda, acertar pela metade a terceira e quarta e acertar a última? Então teremos:
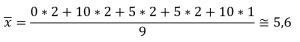
Você também pode gostar de ler:
Expressões Numéricas – O que são? Regras, Ordem das operações e Exercícios
Referências
MEDHI, Jyotiprasad. Statistical methods: an introductory text. New Age International, 1992.
