Na matemática, quando lidamos com uma grande quantidade de números que representam algo, e queremos que essa representação seja reduzida a apenas um número, podemos calcular a medida de tendência central.
Por exemplo, se temos acesso a várias temperaturas que ocorreram em um mês qualquer, podemos encontrar uma única temperatura que represente todo esse período. O número obtido é a medida da tendência central dos vários números usados. A média aritmética é a mais conhecida entre as medidas de tendência central, mas, além dela, também usamos a mediana e a moda. Entenda mais a respeito de cada uma a seguir, só aqui no Gestão Educacional!
Média aritmética
Considerando um grupo de pessoas com 22, 20, 21, 24 e 20 anos, observamos que:
- MA = (22 + 20 + 21 + 24 + 20)/ 5 = 21,4.
Dizemos, então, que a média aritmética, ou simplesmente a média de idade do grupo, é 21,4 anos.
No caso de um aluno que realizou diversos trabalhos durante o bimestre e obteve as notas 7,5; 8,5; 10,0 e 7,0, observamos que:
- MA = (7,5 + 8,5 + 10 + 7)/4 = 8,25.
Assim, generalizando, podemos afirmar que, dados os n valores x1, x2, x3, …, xn de uma variável, a média aritmética é o número obtido da seguinte forma:
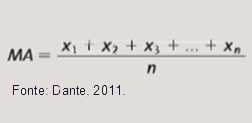
Ou seja, basta somar todos os valores obtidos e dividir pela quantidade de valores somados.
A média aritmética é usada como medida de tendência central, ou seja, como forma de, por meio de um único número, dar uma ideia das características de determinado grupo de números.
No entanto, é importante ressaltar que, em algumas situações, a presença de um valor bem maior ou bem menor do que os demais faz com que a média aritmética não consiga traçar o perfil correto do grupo.
Consideremos, por exemplo, um grupo de pessoas com idades de 2, 3, 2, 1, 2 e 50 anos. A média de idade, que é de 10 anos, não demonstra as características desse grupo em termos de idade. Em casos como esse são usadas outras medidas de tendência central, como a mediana e a moda.
Média aritmética ponderada
Vejamos, agora, o caso de um aluno que realiza vários trabalhos com pesos diferentes, isto é, com graus de importância diferentes. Se, no decorrer do bimestre, ele obteve 6,5 na prova (peso 2), 7,0 na pesquisa (peso 3), 6,0 no debate (peso 1) e 7,0 no trabalho de equipe (peso 2), a sua média, que nesse caso é chamada média aritmética ponderada, será:
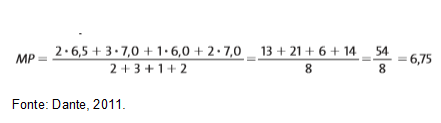
Mediana
A presença de valores que destoem dos demais, por serem muito grandes ou muito pequenos, distorce a média aritmética, fazendo com que ela não caracterize de forma eficiente o conjunto de valores.
Por esse motivo, é conveniente definirmos outra medida de tendência central, a mediana.
Assim, dados n números em ordem crescente ou decrescente, a mediana será:
- O número que ocupar a posição central se n for ímpar;
- A média aritmética dos dois números que estiverem no centro se n for par.
Por exemplo, em uma classe, foram anotadas as faltas durante um período de 15 dias: 3, 5, 2, 0, 2, 1, 3, 4, 5, 7, 0, 2, 3, 4 e 7. Em ordem crescente, temos:
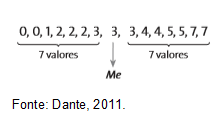
Como 15 é ímpar, o termo médio é o 8º. Logo, a mediana é 3.
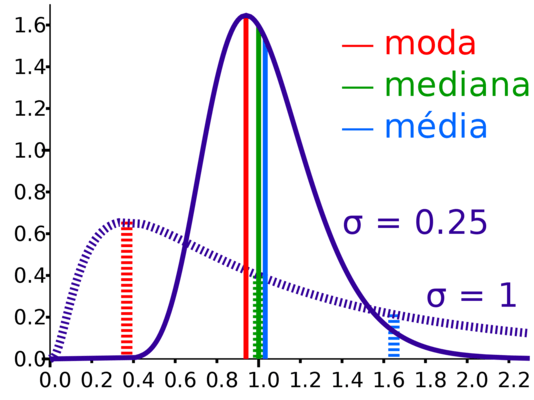
Moda
Em Estatística, moda é a medida de tendência central definida como o valor mais frequente de um grupo de valores observados.
Por exemplo, se temos um grupo de pessoas com idades de 2, 3, 2, 1, 2 e 50 anos, a moda é 2 anos. Esse valor demonstra mais eficiência para caracterizar o grupo que a média aritmética.
Outro exemplo seria encontrar a moda da temperatura medida de hora em hora, das 6h às 11h. Nesse dia, os resultados foram: 14°C, 15°C, 15°C, 18°C, 20°C e 25°C, então dizemos que nesse período a moda foi 15°C.
Se as notas obtidas por um aluno foram 6,0; 7,5; 7,5; 5,0; e 6,0, dizemos que a moda é 6,0 e 7,5 e que a distribuição é bimodal.
Quando não há repetição de números, como para os números 7, 9, 4, 5 e 8, não há moda e a distribuição é chamada amodal.
Exercícios Resolvidos
1) As idades dos alunos de uma equipe são 12, 16, 14, 12, 13, 16, 16 e 17 anos. Encontre a mediana desses valores
RESPOSTA: as idades dos alunos de uma equipe são 12, 16, 14, 12, 13, 16, 16 e 17 anos. Para determinar a mediana desses valores, colocamos inicialmente na ordem crescente (ou decrescente):

Como temos um número par de valores (8), fazemos a média aritmética entre os dois centrais, que são o 4º e o 5º termos. Logo, a mediana é dada pela média aritmética.
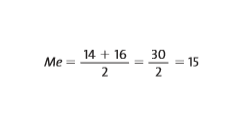
R: 15 ANOS.
