O lançamento oblíquo é um movimento caracterizado por ser bidimensional, ou seja, um movimento tanto vertical quanto horizontal, uma vez que a combinação de ambos acaba gerando um movimento oblíquo.
Temos, então, um lançamento oblíquo quando um objeto é lançado entre um ângulo maior que 0 graus e menor que 90 graus, pois a combinação do movimento vertical e horizontal acabar resultando em um movimento na diagonal.
Quando isso ocorre, por conta da gravidade, o objeto lançado e puxado para baixo, formando uma trajetória parabólica: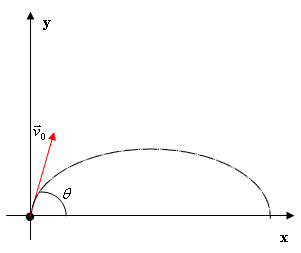
Exemplos de movimento oblíquo
Exemplos de lançamentos oblíquos na prática podem ser os seguintes:
- Arremesso de dardo;
- Movimento da bola em jogos de futebol, vôlei, e outros esportes;
- Movimento de uma flecha, etc.
Como calcular o movimento oblíquo?
A maneira de entender tal tipo de lançamento é realizando o processo de separação entre o movimento horizontal e o movimento vertical. Por exemplo, se há um objeto que foi lançado na diagonal, ocorre um movimento tanto para frente quanto para cima, dessa forma, devemos analisar o quão rápido ele está se movendo para cima e para frente.
A partir disso, há a existência de um componente horizontal da velocidade, articulado pelo eixo X de um plano, ou seja, um Vx, além da existência de um componente vertical da velocidade, articulado pelo eixo Y, assim, Vy.
O movimento horizontal no lançamento oblíquo
O movimento horizontal do lançamento oblíquo pode ser obtido pelo movimento retilíneo uniforme (MRU), uma vez que a velocidade no sentido horizontal não muda, pois não sofre influência da aceleração da gravidade. Além disso, é a partir desse movimento retilíneo uniforme que o alcance máximo pode ser calculado, pois este relaciona-se ao movimento horizontal.
As fórmulas para o cálculo desse movimento são as seguintes:
- Sx= S0x + Xx. t
Tal fórmula representa uma relação do espaço com o tempo a partir de uma velocidade constante, sendo utilizada para descobrir a posição do eixo x, em que cada partícula da fórmula representa as seguintes informações:
- Sx= posição no eixo x;
- S0x = posição inicial no eixo x;
- vx= velocidade do corpo no eixo x;
- t = intervalo de tempo entre o início do movimento até a posição Sx.
- Sx= v. cos (θ). T
Essa fórmula, por sua vez, apresenta a relação entre o alcance de um corpo em lançamento oblíquo, além da velocidade de tal corpo. Sendo cada elemento da fórmula, os seguintes:
- Sx = posição no eixo x;
- V = velocidade do corpo;
- t = intervalo de tempo entre o início do movimento até a posição Sx;
- cos (θ)= cosseno do ângulo.
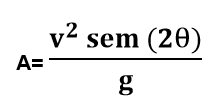
Essa fórmula representa e determina o alcance máximo, sendo cada elemento:
- A= é o alcance máximo do corpo;
- g= é a aceleração da gravidade;
- v = é a velocidade do corpo;
- θ = é o ângulo entre o vetor velocidade de lançamento e o solo;
Além disso, a partir dessa fórmula, podemos concluir que:
- os ângulos complementares são aqueles que, somados, resultam em 90º, tendo sempre o mesmo valor de alcance máximo;
- o maior alcance que o objeto pode atingir é sempre com um ângulo de lançamento de 45º, que resulta em seno de 90º, que possui o valor máximo, no caso, 1.
O movimento vertical no lançamento oblíquo
O movimento vertical do lançamento oblíquo pode ser obtido por meio do movimento uniformemente variado (M.U.V.), já que esse movimento sofre influência da aceleração da gravidade.
As fórmulas para o cálculo desse movimento são as seguintes:
- vy = voy + 2.g. Δ
Esta representa a Fórmula de Torricelli, com a qual é possível calcular a velocidade final de um corpo em movimento retilíneo uniformemente variado, em que:
- vy = a velocidade no eixo y;
- voy= a velocidade inicial no eixo y;
- g = a aceleração da gravidade;
- Δy = o intervalo de tempo entre o início do movimento até a posição Sx.

Essa fórmula calcula a altura máxima atingida pelo corpo, sendo cada elemento:
- H = a altura máxima;
- vo = a velocidade inicial;
- g = a aceleração da gravidade;
- θ = o ângulo entre o vetor velocidade de lançamento e o solo.
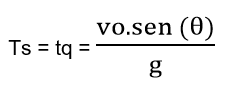 Com essa fórmula, é possível calcular o tempo de subida, que é igual ao tempo de queda, em que:
Com essa fórmula, é possível calcular o tempo de subida, que é igual ao tempo de queda, em que:
- ts = o tempo de subida;
- tq = o tempo de queda;
- vo = a velocidade inicial;
- g = a aceleração da gravidade;
- θ = o ângulo entre o vetor velocidade de lançamento e o solo.
Exercícios Resolvidos
1. (Uefs-BA) Em um planeta X, uma pessoa descobre que pode pular uma distância horizontal máxima de 20,0 m se sua velocidade escalar inicial for de 4,0 m/s. Nessas condições, a aceleração de queda livre no planeta X, em 10–1 m/s2, é igual a
a) 10,0
b) 8,0
c) 6,0
d) 4,0
e) 2,0
Resolução:
Como já explicitado anteriormente, o maior alcance que o objeto pode atingir é sempre com um ângulo de lançamento de 45º, dessa forma, podemos deduzir que essa informação está implícita no enunciado.
Além disso, temos a informação da distância máxima de 20m e da velocidade do corpo, que é igual a 4m/s. Assim, podemos calcular a aceleração de queda livre no planeta a partir da fórmula de alcance máximo:
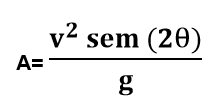
Em que:
A= 20
V= 4
Sen = 45º
Colocando na fórmula e desenvolvendo-a: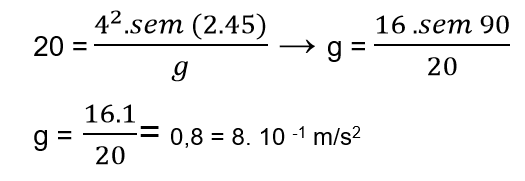
Dessa forma, a alternativa correta é B.
2. (Ufsm-RS) Um índio dispara uma flecha obliquamente. Sendo a resistência do ar desprezível, a flecha descreve uma parábola num referencial fixo ao solo. Considerando o movimento da flecha depois que ela abandona o arco, afirma-se:
I. A flecha tem aceleração mínima, em módulo, no ponto mais alto da trajetória.
II. A flecha tem aceleração sempre na mesma direção e no mesmo sentido.
III. A flecha atinge a velocidade máxima, em módulo, no ponto mais alto da trajetória.
Está(ão) correta(s)
a) Apenas I
b) Apenas I e II
c) Apenas II
d) Apenas III
e) I, II e III
Resolução:
I – Falso, uma vez que a aceleração é constante.
II – Correta, pois, como já vimos nas explicações, a direção sempre será a mesma e no mesmo sentido.
III – Falso, no ponto mais alto a velocidade é mínima.
Alternativa C.

