Costuma-se chamar de lançamento vertical o movimento de um projétil lançado verticalmente para cima. Na verdade, desprezando a resistência do ar, trata-se de um movimento de queda livre. Esse movimento, junto com a queda livre, faz parte dos movimentos sob ação da gravidade.
Desprezando a resistência do ar, todos os corpos cairão no planeta Terra com uma aceleração constante: a aceleração da gravidade. Com uma boa aproximação, podemos dizer que a aceleração gravitacional é de 10m/s².
O que é lançamento vertical?
Podemos dizer que o objeto começa a “cair”, ou seja, sua velocidade se reduz desde o início de seu lançamento, pois ele está sujeito à aceleração da gravidade.
Portanto, todas as funções que descrevem o movimento são as mesmas, desde que se mantenha o mesmo referencial: eixo verticalmente orientado para cima com origem fixada no solo.
Assim, a velocidade do projétil será positiva na subida e negativa na descida, mas a aceleração da gravidade jamais será negativa, pois o sentido dessa aceleração nunca muda, é sempre orientado para baixo.
Ao atingir altura máxima, o projétil para, ou seja, sua velocidade é nula, mas a aceleração continua a mesma. Se jogarmos uma bola de basquete para cima, ela irá subir até uma determinada altura, e depois começará a cair em movimento de queda livre. Portanto, as mesmas equações que vamos utilizar para a queda livre serão empregadas no movimento vertical.
Como nesse movimento a trajetória é retilínea e a aceleração é constante, podemos dizer que ele é um MRUV. Então, para trabalhar com problemas que envolvam o movimento vertical, precisamos reescrever as funções do MRUV. Teremos o seguinte:
- Função da velocidade em relação ao tempo:
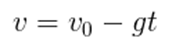
- Função da posição em relação ao tempo:
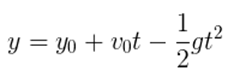
- Função da velocidade em relação à posição (Torricelli):
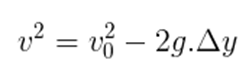
Podemos entender melhor quais são as diferenças das equações acima das equações tradicionais do MRUV com os tópicos abaixo:
- Como a trajetória é sempre na vertical, não usamos mais a variável x para representar a posição do objeto. Portanto, agora a posição do objeto em queda livre fica associada à variável y, relacionada ao eixo vertical das ordenadas;
- A aceleração sempre será a gravidade. Portanto, perceba que em todas as equações acima usamos a = g. Como a aceleração da gravidade é orientada sempre para baixo, o seu valor será negativo. Perceba que alguns sinais foram trocados;
- O deslocamento no MRUV é dado por Δx = x – x0. Porém, agora na queda livre, esse deslocamento será substituído pela altura h ou por Δy = y – y0.
Lançamento vertical para cima
Quando jogamos um objeto para cima, o movimento será acelerado, porém negativo, pois a ação da gravidade faz com que, desde o início, o objeto esteja “caindo”. Com isso, nesse caso, sabemos que a gravidade (g) será negativa.
Lançamento vertical para baixo
No lançamento vertical para baixo, o movimento é acelerado, seguindo o sentido da ação da gravidade. Chamamos o lançamento vertical para baixo de queda livre.
Se não houvesse a resistência do ar, todos os corpos de qualquer peso ou qualquer forma, ao serem abandonados da mesma altura, levariam o mesmo tempo para atingir o solo. Esse tipo de movimento, que consiste em soltar um objeto de uma determinada altura até que ele atinja o chão, é chamado de queda livre.
Quando um corpo é solto de determinada altura, ele adquire um movimento de queda livre em trajetória vertical. Sua velocidade, portanto, aumenta uniformemente com o tempo, e sua aceleração é constante, pois é a aceleração gravitacional que está agindo sobre ele.
Exercício resolvido
1) Um projétil é lançado do solo verticalmente para cima, com velocidade de 40 m/s. Admitindo g = 10 m/s² e desprezando a resistência do ar, determine:
A) a função da posição.
B) a posição no tempo t = 8 s.
C) a função da velocidade.
D) a altura máxima atingida.
E) o instante em que o projétil atinge o solo.
RESOLUÇÃO
A)
Y = Yo – Vot – ½gt²
Y = 40t – 5t²
B) y = 40.8 = 5.8² = 0 m
C) V = Vo – gt
V = 40 – 10t
D) A altura máxima corresponde ao momento em que o objeto para. Portanto, ela ocorre quando v = 0.
Temos:
V² = vo² – 2g(y-yo)
0 = 1 600 – 20y
Y = 80m
E) Quando ele atinge o solo, sua posição é y = 0.
Y = 40 – 5t²
0 = 40 – 5t²
t = 0 e t = 8.
Como t = 0s é o instante de lançamento, t = 8s é quando ele atinge o solo.

