No dia a dia, às vezes, lidamos com situações que envolvem grandezas que não são inteiras. Ou seja, precisamos representar partes de quantidades inteiras. Por exemplo, ao ir comprar algo, usamos os centavos, que são partes do real, para fazer pagamentos.
Nesse contexto, surgem as frações: elas representam os números decimais, que chamamos popularmente de números com vírgula. A seguir, veja como efetuar as operações de multiplicação e divisão de frações, só aqui, no Gestão Educacional!
Multiplicação com frações: o que é?
Quando você adquire um produto, para saber o valor que irá pagar, deve multiplicar a quantidade comprada pelo preço unitário. Por exemplo, 3 quilos de carne a R$12,00 o quilo, custam 3 x 12 = 35 reais.
Que cálculo você faria se comprasse uma quantidade fracionária? Por exemplo, quanto custaria ¾ quilos dessa carne? Como essa situação é equivalente à anterior, nós também multiplicamos ¾ por 12. Qual será o resultado dessa multiplicação?
Se você compra ¾ do quilo, deve pagar ¾ do preço de um quilo, isto é, ¾ de 12.
Ou seja, com isso, você pode perceber 3/4 x 12 e ¾ de 12 são a mesma coisa! Aplicando isso, podemos resolver qualquer multiplicação que envolva frações.
Exemplificando o cálculo com frações
Vamos, então, multiplicar as frações 1/3 e 1/4.
Podemos fazer uma generalização para efetuar esse cálculo, formando, então, uma regra prática geral para fazer multiplicações de frações de forma automática.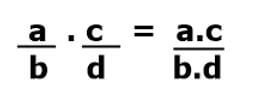
Portanto, para multiplicar frações, devemos multiplicar numerador por numerador e denominador por denominador.
Lembre-se: os números b e d não podem ser igual a zero, pois não existe divisão de um número por 0.
Voltando ao exemplo, o resultado de 1/3 x 1/4 = 1/12.
Dicas para multiplicação com fração
Quando queremos multiplicar uma fração por um número inteiro, podemos pensar da seguinte maneira:
Todo número inteiro pode ser escrito como uma fração. Por exemplo, 7 pode ser escrito como 7/1, pois todo número dividido por 1 resulta nele mesmo.
Antes de efetuar uma multiplicação, podemos utilizar a simplificação para facilitar nossos cálculos. Podemos fazer o mesmo na multiplicação de frações.
Por exemplo: 3/10 x 10/11. Nesse caso, podemos simplificar essa conta.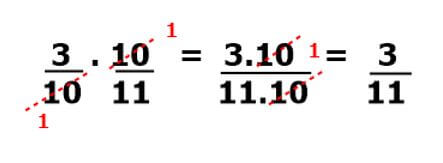
Observando a imagem acima, podemos simplificar dividindo por 10 ou perceber que 10/10 = 1.
Ao simplificar, costumamos dizer que “cancelamos” certos números, por isso acabamos cortando o número com um traço, como feito no exemplo.
Fração inversa
Chamamos de fração inversa a fração que, multiplicada por outra, resulta em 1. Por exemplo, a fração p/q tem inversa q/p.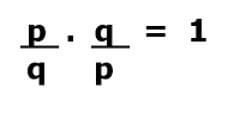
Outro exemplo: a fração inversa de 2/3 é 3/2.
Multiplicação de frações negativas
Para isso, vale relembrar as seguintes regrinhas:
- (Positivo) x (positivo) = (positivo);
- (Negativo) x (negativo) = (positivo);
- (Positivo) x (negativo) = (negativo);
- (Negativo) x (positivo) = (negativo).
Por exemplo: (-7/5) x (1/5) = (-7/25) – (negativo) x (positivo) = (negativo)
Portanto, o resultado dessa multiplicação, por ser um número negativo por um número positivo, deve ser negativo.
Divisão de fração
Usando a propriedade de frações inversas, podemos fazer a divisão de frações. Para fazer essa divisão, iremos usar a seguinte regrinha: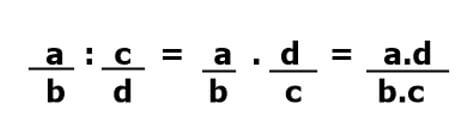
Nesse caso, multiplicamos a primeira fração (a/b) pela fração inversa da segunda.
A inversa da segunda fração (c/d) é igual (d/c). Portanto, vamos multiplicar (a/b) por (d/c), como mostra a imagem acima.
Outro modo de escrever a seguinte situação é: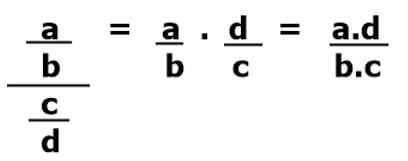
Por exemplo: 5/3 : 2/3 = 5/3 x 3/2 = 15/6.
Exercícios Resolvidos
1) Observe os seguintes modelos de conta:
3/5 x 7 = 3/5 x 7/1 = 21/5
(3/2)² = 3/2 x 3/2 = 9/4
Baseando nesse modelo, efetue as seguintes operações:
a) 4/5 x 10
b) 3/7 x 2/5
RESPOSTA:
a) 4/5 x 10/1 = 40/5 = 8.
b) 3/5 x 2/5 = 6/25
2) Escreva 0,25 na forma de fração e faça as seguintes operações:
a) 0,25 x 3/2 : 1/2
b) 0,25 x 1/3
RESPOSTA:
Primeiramente, vamos transformar 0,25 em fração.
0,25 = 25/100 = 1/4
Agora, vamos realizar as operações.
a) 1/4 x 3/2 = 3/8
3/8 : 1/2 = 3/8 x 2/1 = 6/8 = ¾.
b) 1/4 x 1/3 = 1/12.
3) Complete as lacunas das seguintes frases:
a) Para multiplicar duas frações, basta multiplicar seus ____________ e multiplicar seus _________.
b) O produto de uma fração por sua inversa é igual a ______.
c) Para dividir duas frações, basta multiplicar a primeira pelo ______________.
d) Para encontrar o denominador comum às frações 7/20 e 11/24, podemos calcular ____________.
RESPOSTA:
a) Para multiplicar duas frações, basta multiplicar seus NUMERADORES e multiplicar seus DENOMINADORES.
b) O produto de uma fração por sua inversa é igual a UM.
c) Para dividir duas frações, basta multiplicar a primeira pelo INVERSO DA SEGUNDA FRAÇÃO.
d) Para encontrar o denominador comum às frações 7/20 e 11/24, podemos calcular o MÍNIMO MÚLTIPLO COMUM DOS DENOMINADORES.
