Alguns cientistas trabalham com medidas muito grandes. É o caso de astrônomos, por exemplo, que precisam de muitos algarismos. Com as potências, esses números podem ser escritos de maneira mais curta, facilitando a leitura.
A notação científica é também uma potência, nesse caso, dizemos que notações são potências de base 10. Elas são utilizadas para representar quantias muito pequenas ou muito grandes. Veremos, a seguir, o que são e como realizar operações com notações científicas, só aqui no Gestão Educacional.
O que é notação científica?
Quando escrevemos um número a partir de uma potência de base 10, estamos escrevendo esse número utilizando notação científica.
Nesse tipo de notação, os números têm sempre a seguinte forma:
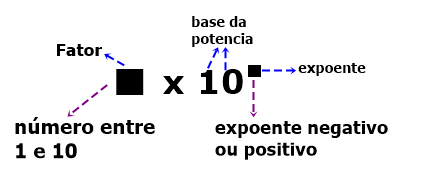
Vamos analisar o seguinte exemplo:
Uma bactéria possui, em média, 0, 000 005 gramas. Esse é um número muito extenso para ser escrito, podemos, então, escreve-lo de outra forma, utilizando notação científica.
Primeiramente, vamos colocar o único algarismo diferente de zero em evidência. Podemos fazer isso da seguinte maneira:
- 0, 000 005 = 5 x 0, 000 001.
Agora, precisamos representar o número 0, 000 001 em uma potência de base 10. Podemos escrever o número 0, 000 001 como o número 10 elevado ao expoente negativo –6.
Portanto, teremos: 0, 000005 = 5.10-6.
Potências com expoentes negativos ou positivos
Quando temos um número que representa valores menores que 1 inteiro, como 0.1, 0.01, entre outros, podemos também escrever os mesmos na forma de potência. Ao passarmos esses valores para forma potencial, colocamos no expoente um número negativo.
Quando uma potência possui o expoente negativo, a propriedade para calcula-la é a seguinte:
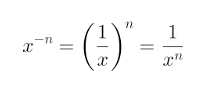
Interpretando essa regra, invertemos a sua base e trocamos o sinal do expoente. Ou seja, o inverso de x seria 1/x. O expoente que antes era –n passa a ser n.
Por exemplo, o número 6^-2 pode ser escrito como:
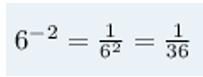
No caso de valores maiores que 1, também podemos representa-los na forma de potência. Observe o seguinte exemplo:
![]()
Perceba que, após o número 2, temos seis números zeros seguidos. Esse valor é exatamente o número do expoente da potência 10!
Operações com notação científica
Para realizar operações com valores muito grandes ou muito pequenos, podemos usar as notações científicas para facilitar a maior parte dos cálculos.
Utilizando sempre potências de base 10, vamos agora descobrir as operações que podemos realizar utilizando notação científica.
Adição e subtração de números com notação científica
Para somarmos dois números que estão representados por notação científica, precisamos nos certificar de que estamos lidando com grandezas de mesmo tamanho. Para isso, devemos ficar atentos ao expoente da base 10.
Podemos somar os números que possuem os mesmos expoentes na potência de base 10. Desse modo, somamos os fatores e mantemos as potências.
De modo geral, na adição, faremos:
![]()
Um exemplo seria:
![]()
De modo análogo, podemos também escrever a regra geral para subtração de números com notação científica:
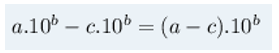
Caso os números envolvidos não estejam com a mesma potência, você deverá deixar os potenciais iguais antes de efetuar os cálculos.
Multiplicação e divisão de números com notação científica
Para efetuarmos a multiplicação de números com notação científica, precisamos lembrar duas propriedades das operações com potências de mesma base:
- Para a multiplicação de potências de mesma base, mantemos o valor da base e somamos os números dos expoentes:
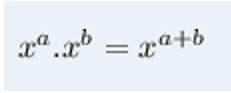
- Para a divisão de potências de mesma base, mantemos o valor da base e subtraímos os números dos expoentes:
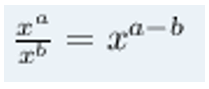
Nesse caso, como estamos lidando com potências de base 10, podemos escrever:
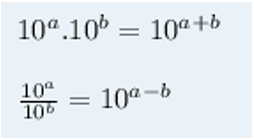
Ou seja, em ambos os casos, mantemos a base 10 e somamos ou subtraímos os expoentes.
Quando a potência é acompanhada de fatores (como 2.10-5, em que o número 2 é o fator), multiplicamos ou dividimos normalmente os fatores e depois fazemos as operações com as potências.
Veja os dois exemplos abaixo:
Exemplo 1: no caso da multiplicação, vamos multiplicar os dois fatores entre si e depois multiplicar as duas potências, usando a propriedade estudada acima.
- (3.102) . (5.106) = (3.5) . (102+6) = 15.108.
Exemplo 2: no caso da divisão, iremos também dividir os dois fatores entre si e depois dividir as potências, aplicando a propriedade estudada acima.
- 102/5.106 = 3/5.102-6 = 0,6.10-4 = 6.10-5.
Exercícios
1) Em 2005, a população do planeta era de aproximadamente 6 500 000 000 de pessoas. Como escrever esse número em notação científica?
RESPOSTA:
Após o último zero, podemos inserir uma vírgula: 6 500 000 000, 0. Para escrever esse número em notação cientifica, vamos “andar” com a vírgula para a esquerda.
Para escrevermos ele como um número entre 1 e 10 multiplicado por uma potência de base 10, faremos o valor 6,5 multiplicado por algo.
Para o número 6 500 000 000, 0 “virar” 6,5, nós “andamos” com a vírgula 9 casas, portanto, a resposta será: 6,5 x 10^9.
