Com o tempo, matemáticos físicos e engenheiros começaram a precisar de um novo conjunto numérico para entender vários fenômenos da matemática. Foi assim que surgiram os primeiros trabalhos feitos por Girolamo Cardano para a elaboração do conjunto dos números complexos.
Leonhard Euler foi um matemático suíço que contribuiu para melhorar a simbologia dos números complexos, atribuindo i para substituir o número √-1. Esse número contribuiu para a resolução de diversos problemas e, atualmente, os números complexos são utilizados em várias áreas da ciência, como mecânica dos fluídos, hidrodinâmica, eletrostática e teoria quântica. Veja, a seguir, o que são números complexos e como utilizá-los.
O que são os números complexos?
Entre os conjuntos numéricos que já conhecemos, tínhamos inicialmente o conjunto dos números naturais, números inteiros, números racionais e números irracionais.
Unindo o conjunto dos números racionais com os números irracionais, surgem os números reais R.
Vamos tentar achar a solução para o seguinte problema:
X² + 1 = 0
X² = -1
X = ±√-1
Sabemos que, se x ∈ R, então x² ≥ 0. Assim, essa equação não tem solução nos números reais, ou seja, não existe número real x elevado ao quadrado que resulte em -1.
Por isso, temos de estender o conjunto dos números reais para obter um conjunto chamado de números complexos (C).
Conjunto dos números complexos
O conjunto dos números complexos é um conjunto do qual podemos extrair a raiz quadrada de um número negativo.
Os números reais são elementos dos números complexos, ou seja, os reais são subconjunto dos números complexos.
A notação que usamos para definir os números complexos z é a forma algébrica ou a forma binomial: z = a + bi – sendo a ∈ R e b ∈ R (pertencentes aos reais R).
Observe que um número complexo escrito dessa forma tem duas partes: uma parte real e uma parte imaginária, como mostra a imagem abaixo: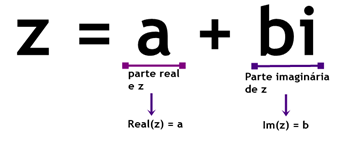
i é a unidade imaginária, tal que i² = -1. É exatamente a existência disso que permite, nesse conjunto, que exista a raiz de um número negativo.
Por exemplo, se x ∈ C e x² = -1, então x = ±1i, -1 = (i²).1 = (1i)².
Assim, conseguimos resolver o problema que observamos no começo!
Denominações para números imaginários:
- Se um número complexo tem unidade imaginaria (b≠0), ele é chamado de imaginário;
- Se b=0, temos que z = a, então z é um número real;
- Se a = 0 e b≠0, temos que z = bi, então z é um imaginário puro.
Operações com números complexos
Usando a forma algébrica que vimos acima, podemos fazer adição, subtração e multiplicação entre números complexos, basta aplicar a propriedade distributiva usada em multiplicação de binômios.
Veja os exemplos abaixo:
- Adição: (2 + 3i) + (-3+4i) = (2-3) + (3i+4i) = -1+7i;
- Subtração: (1+i) – (3+2i) = (1-3) + (1i-2i) = -2 –i;
- Multiplicação: (1+2i) . (2-3i) = (1.2) + (1.(-3i)) + (2i.2) + (2i.(-2i)) = 2 – 3i + 4i -6i² = 8+i (lembre-se que i² = -1).
Conjugado, potência e igualdade de um número complexo
- O conjugado de um número complexo z = a + bi é dado por:
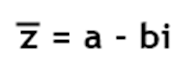
- Dois números complexos z = a + bi e w = c + di são iguais se e somente se a=c e b=d.
Potências de i com expoentes inteiros podem assumir apenas 3 valores: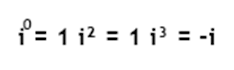
A partir disso, esses valores começam a se repetir. Portanto, para saber o resultado de i elevado a um número qualquer, faça:
Módulo e forma trigonométrica de um número complexo
Dado um número complexo z = a+bi, dizemos que o seu módulo é calculado por: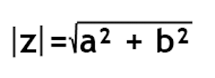
Esse módulo é também chamado de argumento de z.
Para encontrarmos a forma trigonométrica de um número complexo, utilizamos a seguinte fórmula: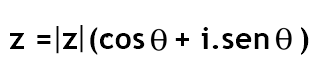
Sendo:
- 0 ≤ θ ≥ 2π
- cos θ = a \ |z| (a dividido pelo módulo de z)
- Sen θ = b / |z|
Potenciação de números complexos na forma trigonométrica
A potência zn (sendo n um número real positivo) é dada pela fórmula de Moivre, que veremos a seguir: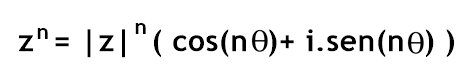
Para n = 0, z0 = 1.
Exercício resolvido
1) Determine a forma trigonométrica do seguinte número complexo z = 1 + i
RESOLUÇÃO:
Se z = 1+1, temos que a=1 e b=1
|z| = √(1²+1²) = √2
Calculando o argumento θ, teremos:
cos θ = 1/√2 = √2/2
Sen θ = 1/√2 = √2/2
Com isso, sabemos que o ângulo em que o seno e o cosseno resultam em √2/2 é o ângulo θ = π/4. Caso você tenha dificuldade nisso, use uma calculadora científica e calcule o arcsen √2/2 ou o arccos √2/2, e confira nosso conteúdo completo sobre seno, cosseno e tangente, clicando aqui.
Assim, a forma trigonométrica de z é dada por:
Z = √2.(cos π/4 + i.sen π/4).
