Para entendermos o conceito de números inteiros, vamos retomar o que são os números naturais. Vamos considerar o seguinte exemplo: João ganhou de sua mãe um punhado de balas e, para contar essas balas, ele irá utilizar números reais inteiros. João, portanto, está utilizando números naturais para contá-las – N = {0,1,2,3…}.
Agora, vamos imaginar outra situação. Certo condomínio registrava uma receita R de R$12.800, despesas D no valor de R$13.000. Para encontrarmos o Saldo S, temos que fazer R-D.

Ao realizar essa operação, percebemos que a receita foi menor que as despesas, portanto, não existe um número natural que represente esse saldo S.
Surge, então, a necessidade de um número que não seja natural, um número que então seja negativo e que represente a dívida de R$200 que o condomínio tem.
Definição de números inteiros
O conjunto dos números é então a junção dos números naturais e os números inteiros negativos. Indicamos o conjunto dos números inteiros por Z.
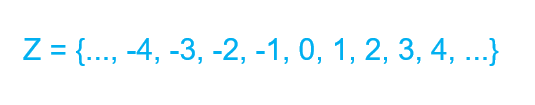
Temperaturas, por exemplo, podem ser representadas por números inteiros, como 3°C.
Ideia de conjunto e características
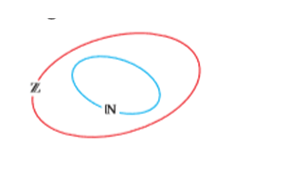
Podemos dizer, então, que os números naturais são um subconjunto dos números inteiros. Ou seja: Z⊃N. Consequentemente, todo número natural é inteiro. Podemos representar isso no diagrama abaixo:
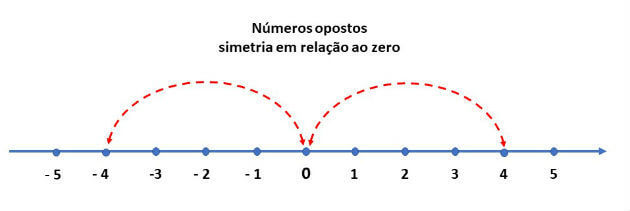
Há em Z uma certa simetria em relação ao número 0. Por exemplo, o oposto ou simétrico de 3 é o –3, valendo: -3 + 3 = 0. Portanto, a soma desses opostos resulta em 0.
No conjunto Z é sempre possível efetuar a adição, a multiplicação e a subtração. Consequentemente, a soma, o produto e a diferença de dois números inteiros resultam sempre em um número inteiro. E todas as propriedades das operações em N continuam válidas em Z.
Porém, não podemos aplicar essa mesma regra para a divisão de dois números inteiros: nem sempre a divisão de dois números inteiros resulta um número inteiro.
Por exemplo: (-7) / (2) não é possível em Z.
Notações especiais
- Notação Z* é usada para representar números inteiros não nulos Z* = {…, -3, -2, -1, 1, 2, 3, …};
- Notação Z+ é usada para representar o conjunto dos números inteiros não negativos Z+ = {0, 1, 2, 3, 4, 5, 6, …};
- Notação Z*+ representa números inteiros positivos Z*+ = {1, 2, 3, 4, …};
- Notação Z- descreve o conjunto dos números inteiros não positivos Z- = {…, -4, -3, -2, -1, 0};
- Notação Z*- representa inteiros negativos Z*- = {…, -4, -3, -2, -1}.
Números consecutivos, antecessor e sucessor
Se n é um número inteiro, então n+1 é inteiro tal que:
- n e n+1 são chamados de inteiros consecutivos;
- n é antecessor de n+1;
- n+1 é sucessor de n.
Números pares e ímpares
Dizemos que um número inteiro é par se, e somente se, pode ser representado sob a forma 2n, com n ∈ Z. Por exemplo: o número 6 é par, pois podemos representá-lo por 2 x 3 e 3 ∈ Z.
Por outro lado, um número inteiro é ímpar se, e somente se, pode ser representado sob a forma de 2n+1, com n ∈ Z. Por exemplo: o número -15 é ímpar, pois pode ser representado por 2 x (-8) e –8 ∈ Z.
Propriedades dos números inteiros
- P1 – Sendo P e I o conjunto dos números inteiros pares e ímpares, respectivamente, temos P ∪ I = Z e P ∩ I = Ø;
- P2 – Todo número inteiro tem sucessor e antecessor;
- P3 – A soma de dois números inteiros quaisquer é um número inteiro;
- P4 – A diferença entre dois números inteiros quaisquer é um número inteiro;
- P5 – O produto de dois números inteiros quaisquer é um número inteiro.
Exercícios Resolvidos
1) Sendo a e b números inteiros tais que a + b é um número par, prove que a² – b² é um número par.
___________________________
___________________________
2) Classifique como par ou ímpar:
A) 2n
B) 2n+1
C) 4n + 1
D) 8n + 3
RESPOSTA:
1. Como, por hipótese, a+b é par, podemos afirmar que a+b = 2k, com k ∈ Z. Assim, teremos: a²-b² = (a+b)(a-b) = 2k.(a-b).
Pelas propriedades 4 e 5 descritas acima, k(a-b) é um número inteiro, então 2k(a-b) é par e, portanto, a²-b² é par.
2. A) par B) ímpar C) ímpar D) ímpar.
