Os números primos são aqueles que possuem apenas dois divisores: ele mesmo e o número 1. Ao tentar dividir esse número por outros valores, você não irá obter como resultado um número inteiro, ou seja, o resultado terá casas decimais.
A seguir, iremos definir e aprender a como identificar números primos.

Divisores de um numero natural
Para entendermos o que são números primos, vamos definir primeiramente o que são os divisores de um número natural.
Vamos imaginar a seguinte situação: Dona Maria tem 12 pães e pretende distribui-los em caixas, de modo que as caixas devem conter a mesma quantidade de pães e nenhum pão pode sobrar fora dela.
Para isso, Dona Maria possui as seguintes opções:
- Usar uma caixa com os dois pães. Observe que 12 ÷ 1 = 12;
- Usar duas caixas contendo 6 pães cada. Observe que 12 ÷ 2 = 6;
- Usar três caixas contendo 4 pães cada. Observe que 12 ÷ 3 = 4;
- Usar quatro caixas contendo 3 pães cada. Observe que 12 ÷ 4 = 3;
- Usar 6 caixas contendo 2 pães cada, 12 ÷ 6 = 2;
- Usar, por fim, 12 caixas contendo um pão cada, 12 ÷ 12 = 1.
Conseguimos resolver o problema de Dona Maria de 6 maneiras diferentes. Com isso, percebemos que podemos dividir 12 pães de 6 maneiras diferentes, ou seja, o número 12 possui 6 divisores.
Dizemos, portanto, que 1, 2, 3, 4, 6 e 12 são divisores de 12, pois a divisão de 12 por cada um desses números resta 0.
O que são números primos?
Vamos prestar atenção em outro exemplo:
Tenho 7 chocolates e quero dividi-los em caixas. Para isso, tenho apenas duas possibilidades:
- Usar uma caixa e colocar 7 chocolates nela;
- Usar 7 caixas e colocar 1 chocolate em cada.
Perceba que o número 7 possui apenas dois divisores: 1 e ele mesmo. 7 é, então, um número que chamamos de primo.
Portanto, número primo é todo número natural maior do que 1, que tem exatamente dois divisores: o 1 e ele mesmo.
Exemplos
- Três (3) é um número primo, pois é maior do que 1 e tem apenas 1 e 3 como seus divisores. Ou seja, caso quiséssemos dividir 3 por 2, teríamos o resultado de 1,5 (3 ÷ 2 = 1,5).
Dois, então, não é um divisor de 3 pois o resultado dessa divisão não deu um número inteiro.
No caso, 1,5 é um número racional.
- Vinte e quatro (24) não é um número primo, pois ele tem mais que dois divisores;
- zero (0) não é um número primo, pois além de não ser maior que 1, ele tem infinitos divisores;
- O número um (1) não é um número primo, pois ele não é maior do que 1 e, além disso, tem apenas 1 divisor, ele mesmo;
- O número 2 é o único número par primo;
- O número 5 é o único número natural terminado em 5 que é primo.
Crivo de Eratóstenes
Para saber quais são os números primos até 100, podemos fazer a seguinte lição: escreva todos os números que vão de 1 até 100. Risque os múltiplos de 2, 3, 5 e 7 maiores que eles
Você irá obter algo semelhante à imagem abaixo.
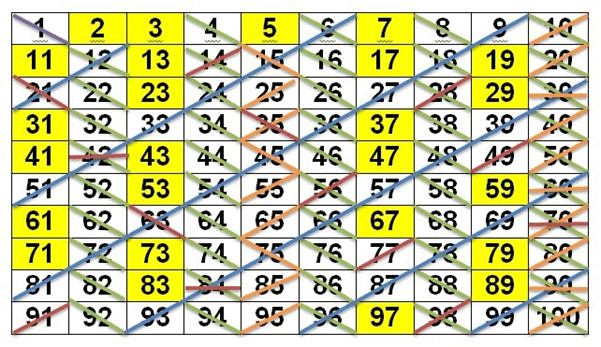
Os números destacados em amarelo, que são os que não foram riscados em nenhum momento, são os números considerados primos de 1 até 100.
Perceba que, quando um número pode ser obtido pela multiplicação de dois (ou mais) números primos, ele não é um número primo! Por exemplo, 4 pode ser obtido por 2×2 = 4. Portanto, 4 não é primo!
Enquanto isso, 7 só pode ser obtido ao multiplicar 7×1 = 7, sendo o número 1 um número que não é primo. Portanto, 7 é primo.
Decomposição em fatores primos
Para decompor um número natural maior do que 1 que não é primo em fatores primos, utilizamos o processo de fatorações sucessivas.
Podemos definir que todo número maior do que 1 que não é primo pode ser decomposto em um produto de dois ou mais fatores primos.
Veja um exemplo a seguir:
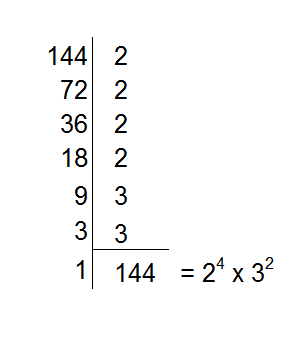
Comece fazendo a divisão de 144 pelo menor primo possível, que no caso é o 2. Continue fazendo isso até que a próxima divisão não dê um número inteiro. No caso, quando chegamos em 9, não conseguimos dividi-lo por 2, pois não resultaria em um número inteiro.
Quando chegamos a esse ponto, comece as divisões pelo próximo menor primo possível, que no caso é o número 3.
Quando há fatores repetidos em uma fatoração, podemos usar a potenciação para simplificar a escrita.
Perceba que: 144 = 2 x 2 x 2 x 2 x 3 x 3 = 3² x 24
Números primos entre si
Dizemos que dois números são primos entre si quanto os únicos divisores que eles possuem em comum é o número 1.
Por exemplo, os números 2 e 3 são primos entre si:
- Divisores de 2: 1 e 2;
- Divisores de 3: 1 e 3;
- Divisores em comum: apenas o número 1.
Agora que você já sabe um pouco mais a respeito dos números primos, que tal testar os seus conhecimentos nos exercícios que preparamos para você? Basta rolar até o final da página e se divertir! Ah, e não deixe de compartilhar com os seus amigos, desafiando eles também.
